Question

Find an equation of the line

parallel to y = 4x + 5 and
that passes through the point
(-2,5)

Answer 1

`\mathrm{We\ have,}\\y=4x+5......(1)\\\mathrm{Comparing\ with}\ y=mx+c,\\\mathrm{Slope}(m_1)=4.\\\mathrm{Let\ the\ slope\ of\ the\ line\ parallel\ to\ line(1)\ be\ }m_2.\\\mathrm{Then,\ }m_1=m_2\\\mathrm{or,\ }m_2=4.\\\mathrm{Equation\ of\ a\ line\ passing\ through\ (-2,5)\ and\ slope\ 4\ is\ given\ by:}\\y-5=4(x+2)\\\mathrm{or,\ }y-5=4x+8\\\mathrm{or,\ }y=4x+13\ \mathrm{is\ the\ required\ equation}.`

Answer 2

Equations of straight lines

An equation of a straight line can be written in several forms. The most common way of writing the equation of a straight line is known as Slope-intercept form. The format of this equation is:

`\huge\boxed{\sf{y=mx+b}}`

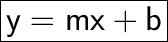
Where:

• m = slope
• b = y-intercept

However, to write the equation in this form, you need to know the slope and the y-intercept. If we're given a point we can plug it into y = mx + b and solve for b. Alternatively, we can use another form called Point - Slope:

`\huge\boxed{\sf{y-y_1=m(x-x_1)}}`

Where:

• m = slope
• (x₁,y₁) = a point on the line

With all this information, we can go ahead and solve.

Our slope, m, is 4, since parallel lines have equal slopes; the slope of y = 4x + 5 is 4, and so is the slope of the line which is parallel to it.

Plug in the data:

`\boxed{\!\!\boxed{\quad\large\begin{gathered}\sf{y-y_1=m(x-x_1)}\\\sf{y-5=4(x-(-2)}\\\sf{y-5=4x+2}\\\sf{y=4x+2+5}\\\sf{y=4x+7}\end{gathered}}\!\!}`

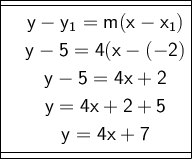
Hence, the equation is y = 4x + 7.

`\rule{350}{4}`

`\frak{-Dream-}`