The exact length of the curve
 over the interval
over the interval
 is given by:
is given by:
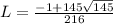
It is approximately
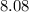 when rounded to two decimal places.
when rounded to two decimal places.
Let's proceed with the solution to find the exact length of the curve
 over the interval
over the interval
 .
.
Step 1: Formula for the Length of a Curve
The length
 of a curve given by
of a curve given by
 from
from
 is calculated using the formula:
is calculated using the formula:
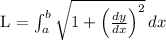
Step 2: Differentiating

First, we need to find the derivative
 .
.

Step 3: Integrating to Find the Length
After finding
 , we will substitute it into the formula for
, we will substitute it into the formula for
 and evaluate the integral from
and evaluate the integral from
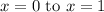 .
.
Let's start by calculating the derivative
 .
.
The derivative
 of
of
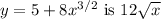 .
.
Step 4: Setting Up the Integral
Now, we substitute this derivative into the formula for the length of the curve:
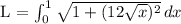
This simplifies to:
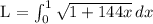
Step 5: Evaluating the Integral
Let's evaluate this integral to find the exact length of the curve.
The exact length of the curve
 over the interval
over the interval
 is given by:
is given by:
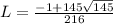
Detailed Evaluation of the Integral
We need to evaluate the integral:

This integral can be solved by making a substitution that simplifies the square root term. Let's use the substitution
 . Then,
. Then,
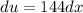 or
or
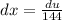 . When
. When
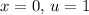 , and when
, and when
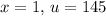 .
.
Substituting these into the integral, we get:

This simplifies to:
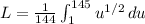
The integral of
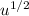 with respect to
with respect to
 is
is
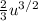 . Applying this to our integral, we get:
. Applying this to our integral, we get:
![L = (1)/(144) \left[ (2)/(3) u^(3/2) \right]_(1)^(145)](https://img.qammunity.org/2024/formulas/mathematics/high-school/g4iuf9q34rng5mv63huii2czav9p0tstdz.png)
Evaluating this from 1 to 145, we have:
![L = (1)/(144) \left[ (2)/(3) (145^(3/2)) - (2)/(3) (1^(3/2)) \right]](https://img.qammunity.org/2024/formulas/mathematics/high-school/xq34bfmvonex6rhqlb2xxseot1pjv9pzmx.png)
Now, let's calculate this value to get the length of the curve up to two decimal places.
The exact length of the curve
 over the interval
over the interval
 is approximately
is approximately
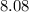 when rounded to two decimal places.
when rounded to two decimal places.