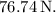Final Answer:
(a) The angular acceleration of the arm is approximately

(b) The force required of the triceps muscle is approximately
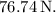
Step-by-step explanation:
(a) The angular acceleration
 can be calculated using the formula
can be calculated using the formula
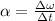 , where
, where
 is the change in angular velocity and
is the change in angular velocity and
 is the change in time. In this case, the ball is released, so the angular velocity
is the change in time. In this case, the ball is released, so the angular velocity
 becomes
becomes
 at the end. The initial angular velocity is
at the end. The initial angular velocity is
 because the ball starts from rest. Therefore,
because the ball starts from rest. Therefore,
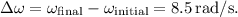 Plugging in the values,
Plugging in the values,
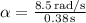 , which gives
, which gives
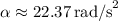 .
.
(b) The force required
 can be found using the equation
can be found using the equation
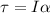 , where
, where
 is the torque,
is the torque,
 is the moment of inertia, and
is the moment of inertia, and
 is the angular acceleration. The moment of inertia for a uniform rod rotating about its end is
is the angular acceleration. The moment of inertia for a uniform rod rotating about its end is
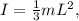 where
where
 is the mass and
is the mass and
 is the length. The torque can be expressed as
is the length. The torque can be expressed as
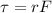 , where
, where
 is the length from the axis to the point where the force is applied. In this case,
is the length from the axis to the point where the force is applied. In this case,
 . Substituting these into the torque equation, we get
. Substituting these into the torque equation, we get
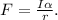 Plugging in the values,
Plugging in the values,
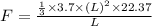 , which simplifies to
, which simplifies to
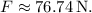
In summary, (a) the angular acceleration of the arm is approximately
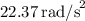 , and (b) the force required of the triceps muscle is approximately
, and (b) the force required of the triceps muscle is approximately