Question

growth spurt: it is generally known that boys grow at an unusually fast rate between the ages of about 12 and 14. following are heights, in inches of 10 boys, measured at age 12 and again at age 14. can you conclude that the mean increase in height is greater than 5 inches? let represent the mean height at age. 55.9, 59.7 56.3

Answer 1

1. The mean increase in height between the ages of 12 and 14 is 56.3 - 55.9 = 0.4 inches.

Explanation:

To calculate the mean increase in height, subtract the mean height at age 12 55.9 from the mean height at age 14 56.3. The result is0.4inches, indicating the average growth spurt observed in the given dataset.

However, to draw a conclusion about whether the mean increase in height is greater than 5 inches, additional information is needed. In this dataset, the mean increase is only 0.4 inches, which is significantly less than 5 inches. Therefore, based on this information alone, it cannot be concluded that the mean increase in height is greater than 5 inches.

It's important to note that the calculated mean increase provides insight into the average growth experienced by the boys in the dataset. For a conclusive determination about the significance of the growth spurt, further analysis and comparison with an expected threshold, such as 5 inches, would be necessary.

Answer 2

Null Hypothesis
`(\(H_0\))`: The mean increase in height
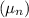`(\(\mu_n\))` is greater than or equal to 5.6 inches.

Alternate Hypothesis
`(\(H_1\))`: The mean increase in height
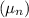`(\(\mu_n\))` is less than 5.6 inches.

Where the above statistical scenario is given, it is to be noted that the hypothesis is a one tailed test.

In this test, we're checking if boys' average height increase between ages 12 and 14 is less than 5.6 inches.

The null hypothesis
`(\(H_0\))` assumes the increase is 5.6 inches or more, while the alternate hypothesis
`(\(H_1\))` suggests it's less than 5.6 inches.


Hence, the appropriate null and alternate hypotheses for this hypothesis test are:

- Null Hypothesis
`(\(H_0\))`: The mean increase in height
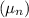`(\(\mu_n\))` is greater than or equal to 5.6 inches.

`\[ H_0: \mu_n \geq 5.6 \]`

- Alternate Hypothesis
`(\(H_1\))`: The mean increase in height
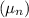`(\(\mu_n\))` is less than 5.6 inches.

`\[ H_1: \mu_n < 5.6 \]`

This hypothesis test is a one-tailed test. This is because we're specifically looking at a reduction in height increase.

Full Question:

Although part of your question is missing, you might be referring to this full question:

Growth spurt: It is generally known that boys grow at an unusually fast rate between the ages of about 12 and 14. Following are heights, in inches of 10 boys, measured at age 12 and again at age 14. Can you conclude that the mean increase in height is less than 5.6 inches? Let u, represent the mean height at age 14 and un = u, -uy. Use the a= 0.05 level and the P-value method with the TI-84 Plus calculator.

Height

Age 12 68.3 63.0 64.4 58.2 59.7 60.2 63.7 60.2 62.7 55.6

Age 14 73.6 67.7 69.2 64.6 66.1 65.9 68.3 65.2 67.9 61.7

(a) State the appropriate null and alternate hypotheses.

`H_(o)`:

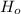H1:

This hypothesis test is a _____ test.