Question

A NASA scientist studies a Moon rock whose mass is9.00 kg and finds that it has an apparent mass of6.50 kg when submerged in water.What is the density of the rock? _______kg/m3This problem has been solved!You'll get a detailed solution from a subject matter expert that helps you learn core concepts.A NASA scientist studies a Moon rock whose mass is9.00 kg and finds that it has an apparent mass of6.50 kg when submerged in water.What is the density of the rock? _______kg/m3

Answer 1

The density of the Moon rock is
`\( 3.6 \, \text{kg/m}^3 \).`

The apparent loss of mass of an object when submerged in a fluid (like water) is due to the buoyant force acting on the object. The weight of the fluid that the object has displaced equals this force.

Given:

- Mass of the rock
`(\( m_{\text{rock}} \)) = 9.00 kg`

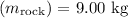
- Rock's apparent mass in water
`(\( m_{\text{apparent}} \)) = 6.50 kg`

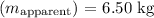
To find the density
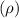`(\( \rho \))` of the rock, we'll use the concept of buoyancy.

The apparent loss in mass
`(\( \Delta m \))` of the rock is due to the buoyant force exerted by the water:

`\[ \Delta m = m_{\text{rock}} - m_{\text{apparent}} \]`

`\[ \Delta m = 9.00 \, \text{kg} - 6.50 \, \text{kg} = 2.50 \, \text{kg} \]`

This
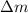`\( \Delta m \)` is the mass of the water displaced by the rock.

The buoyant force
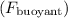`(\( F_{\text{buoyant}} \))` acting on the rock is equal to the weight of the displaced water, which is the same as the apparent loss in mass:

`\[ F_{\text{buoyant}} = \Delta m \cdot g \]`

`\[ F_{\text{buoyant}} = 2.50 \, \text{kg} * 9.81 \, \text{m/s}^2 \]`

`\[ F_{\text{buoyant}} = 24.525 \, \text{N} \]`

The buoyant force
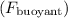`(\( F_{\text{buoyant}} \))` is also equal to the weight of the volume of water displaced by the rock. The volume of water displaced
`(\( V_{\text{displaced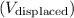}} \))` is the same as the volume of the rock.

Now, using the formula for density:

`\[ \rho = \frac{m_{\text{rock}}}{V_{\text{rock}}} \]`

We know that:

`\[ m_{\text{rock}} = 9.00 \, \text{kg} \]`

`\[ V_{\text{rock}} = \frac{m_{\text{rock}}}{\rho} \]`

So, we can rewrite the density formula in terms of the given values:

`\[ \rho = \frac{m_{\text{rock}}}{V_{\text{rock}}} = \frac{m_{\text{rock}}}{m_{\text{rock}} / \rho} = \rho \]`

Solving for
`\( \rho \):`

`\[ \rho = \frac{m_{\text{rock}}}{\Delta m} \]`

`\[ \rho = \frac{9.00 \, \text{kg}}{2.50 \, \text{kg}} \]`

`\[ \rho = 3.6 \, \text{kg/m}^3 \]`