Question

!50 POINTS! (3 SIMPLE GEOMETRY QUESTIONS)

QUESTIONS BELOW
|
|
\/

Answer 1

1) d. 32.5 ft

2) b. 41cm, 40cm 9cm

3) b. 75 ft

Explanation:

Question 1

The given scenario is modelled as a right triangle, with an interior angle of 38°, and the side opposite the angle measuring 20 ft.

The total length of the six cars of the roller coaster is the hypotenuse of the right triangle.

To find the length of the hypotenuse of the right triangle, we can use the sine trigonometric ratio.

`\boxed{\begin{minipage}{9 cm}\underline{Sine trigonometric ratio} \\\\$\sf \sin(\theta)=(O)/(H)$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf O$ is the side opposite the angle. \\\phantom{ww}$\bullet$ $\sf H$ is the hypotenuse (the side opposite the right angle). \\\end{minipage}}`

Substituting the values into the ratio, we get:

`\sin 38^(\circ)=(20)/(H)`

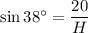
Solving for H:

`H=(20)/(\sin 38^(\circ))`

`H=32.4853849...`

`H=32.5\; \sf (nearest\;tenth)`

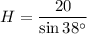
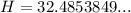
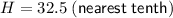
Therefore, the approximate length of the six cars is 32.5 ft.

`\hrulefill`

Question 2

To determine if a triangle is a right triangle, we need to check if it satisfies the Pythagorean theorem, which states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides.

`\boxed{\begin{minipage}{9 cm}\underline{Pythagoras Theorem} \\\\$a^2+b^2=c^2$\\\\where:\\ \phantom{ww}$\bullet$ $a$ and $b$ are the legs of the right triangle. \\ \phantom{ww}$\bullet$ $c$ is the hypotenuse (longest side) of the right triangle.\\\end{minipage}}`

Substitute the given side lengths of each answer option into the formula to see if any of them satisfy the Pythagorean theorem.

Note: As the hypotenuse is the longest side of a right triangle, the value of c should be the longest side.

`\begin{aligned}\textsf{a.} \qquad 50^2+11^2&=52^2\\1500+121&=2704\\2621 &\\eq2704\end{aligned}`

`\begin{aligned}\textsf{b.} \qquad 40^2+9^2&=41^2\\1600+81&=1681\\1681&=1681\end{aligned}`

`\begin{aligned}\textsf{c.} \qquad40^2+35^2&=45^2\\1600+1225&=2025\\2825 &\\eq 2025\end{aligned}`

`\begin{aligned}\textsf{d.} \qquad35^2+25^2&=45^2\\1225+625&=2025\\1850&\\eq2025\end{aligned}`

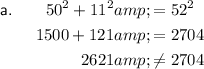
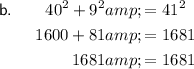
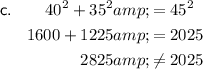
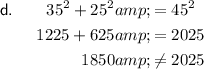
From the above calculations, we can see that option b satisfies the Pythagorean theorem. Therefore, the triangle with side lengths 41 cm, 40 cm, 9 cm is a right triangle.

`\hrulefill`

Question 3

The given scenario is modelled as a right triangle, with an interior angle of 20°, and a hypotenuse measuring 80 ft.

The distance between the two poles is the side of the triangle adjacent to the given angle, labelled "x".

To find the value of x, we can use the cosine trigonometric ratio.

`\boxed{\begin{minipage}{9 cm}\underline{Cosine trigonometric ratio} \\\\$\sf \cos(\theta)=(A)/(H)$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf A$ is the side adjacent the angle. \\\phantom{ww}$\bullet$ $\sf H$ is the hypotenuse (the side opposite the right angle). \\\end{minipage}}`

Substituting the values into the ratio, we get:

`\cos 20^(\circ)=(x)/(80)`

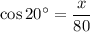
Solving for x:

`x=80\cos 20^(\circ)`

`x=75.17540966...`

`x=75\; \sf ft`

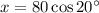
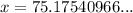
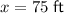
Therefore, the value of x to the nearest whole foot is 75 ft.