Question

!50 POINTS! (3 SIMPLE GEOMETRY QUESTIONS)

QUESTIONS BELOW
|
|
\/

Answer 1

1st picture: d.
`\tt l=7√(2)` cm

2nd Picture: a. 50 in, 48 in, 14 in

3rd picture: c. 21 ft.

Explanation:

For 1st Picture:

Given:

• Diagonal of the square (d) = 14 cm
• Length of side (l) = ?

Note:

• We know that the diagonal of a square bisects into two 45-45-90 right triangles.
• The Pythagorean theorem states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

In this case,

the hypotenuse is the diagonal of the square and the other two sides are the sides of the square.

Solution:

Applying the Pythagorean theorem, we get:

`\tt l^2 + l^2 = d^2`

`\tt 2l^2 = d^2`

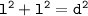
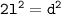
Plugging in the value of the diagonal, we get:

`\tt 2l^2 =14^2`

`\tt l^2=(196)/(2)`

`\tt l=√(98)`

`\tt l=7√(2)`

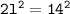
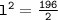
Therefore, the length of the side of the square is d.
`\tt l=7√(2)` cm

`\hrulefill`

For 2nd Picture:

In order to verify this,

we can use the Pythagorean theorem, which states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

c is longest side.

`\boxed{\tt a^2 + b^2 = c^2}`

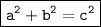
Let's check a.

In this case, we have:

`\tt 48^2 + 14^2 = 50^2`

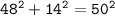
2304+196=2500

2500=2500

Here,

50 cm is the hypotenuse of the triangle, while 48 cm and 14 cm are the other two sides.

Since the left-hand side of the equation is equal to the right-hand side, we can conclude that the triangle is a right-angled triangle.

• The other three triangles are not right-angled triangles because the square of the hypotenuse is not equal to the sum of the squares of the other two sides.

The only right-angled triangle out of the options you provided is a. 50 in, 48 in, 14 in

`\hrulefill`

For 3rd Picture:

Given:

• Hypotenuse of right angle = 25 ft
• One leg = 14 ft
• Other leg = ?

We can use the Pythagorean theorem to solve for the length of the other leg.

The Pythagorean theorem states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

Solution:

Let x be the length of the other leg.

Applying the Pythagorean theorem, we get:

25^2 = 14^2 + x^2

625 = 196 + x^2

x^2 = 625 - 196 = 429

x = \sqrt{429 }

x= 20.7

In nearest tenth

x= 21

Therefore, the length of the other leg is c. 21 ft.