Question

!50 POINTS! (3 SIMPLE GEOMETRY QUESTIONS)

QUESTIONS BELOW
|
|
\/

Answer 1

1) d. 40√2

2) a. 2√41

3) d. 6√2

Explanation:

Question 1

A 45-45-90 triangle is a special type of triangle where the two legs are congruent and the angles opposite those legs are both 45°. The remaining angle, opposite the hypotenuse, is always 90°.

In a 45-45-90 triangle, the ratios of the side lengths are 1 : 1 : √2. This means that the length of the hypotenuse is equal to the length of a leg multiplied by √2.

Given that one leg of the triangle is 40 feet, the length of the hypotenuse is 40√2 feet.

`\hrulefill`

Question 2

To determine the length of the third side of a triangle, we can use the Triangle Inequality Theorem. According to this theorem, the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.

Let "x" be the third side of the triangle. Given the other side lengths are 10 and 8, we can create three inequalities:

`10 + 8 > x`

`10 + x > 8`

`8 + x > 10`

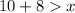
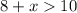
Solve the inequalities:

`18 > x`

`x > 2`

`x > -2`

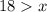
Combining the solutions, the range for the length of the third side is 2 < x < 18.

Therefore, the only answer option that satisfies this interval is 2√41.

`\hrulefill`

Question 3

The sum of the interior angles of a triangle is 180°. Therefore this triangle is a special 45-45-90 triangle.

In a 45-45-90 triangle, the ratios of the side lengths are 1 : 1 : √2. This means that the length of the hypotenuse is equal to the length of a leg multiplied by √2.

Given the leg of the triangle is 6 units, the length of the hypotenuse (x) is 6√2.