Question

Find the x- intercept and the y- intercept of the graph of the equation: 7x+3y=63

Answer 1

x-intercept : 9

y-intercept: 21

Explanation:

Gn: 7x + 3y = 63

The x-intercept is the value of x when y = 0

7x + 3(0) = 63

⇒ 7x = 63

`\implies x = (63)/(7)`

⇒ x = 9

The y-intercept is the value of y when x = 0

7(0) + 3y = 63

⇒ 3y = 63

`\implies y = (63)/(3)`

⇒ y = 21

Answer 2

x-intercept = (9, 0)

y-intercept = (0, 21)

Explanation:

x-intercept

The x-intercept of a linear graph is the point at which the line intersects the x-axis, so when y = 0.

Therefore, to find the x-intercept, substitute y = 0 into the equation and solve for x:

`\begin{aligned}y=0 \implies 7x+3(0)&=63\\7x+0&=63\\7x&=63\\7x / 7&=63 / 7\\x&=9\end{aligned}`

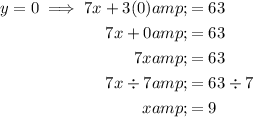
Therefore, the x-intercept of the given equation is (9, 0).

`\hrulefill`

y-intercept

The y-intercept of a linear graph is the point at which the line intersects the y-axis, so when x = 0.

Therefore, to find the y-intercept, substitute x = 0 into the equation and solve for y:

`\begin{aligned}x=0 \implies 7(0)+3y&=63\\0+3y&=63\\3y&=63\\3y / 3&=63 / 3\\y&=21\end{aligned}`

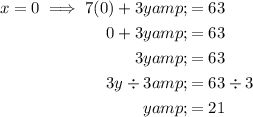
Therefore, the y-intercept of the given equation is (0, 21).