Question

part b: write the midpoint reimann sum that estimates the integral from 1 to 5 of f of x dx, based on the subintervals given in the table. (4 points)

Answer 1

Part A: The right Riemann sum estimate is approximately 22.68.

Part B: The midpoint Riemann sum estimate is approximately 21.31.

Part C: The right Riemann sum estimate is an overestimate based on the properties of the function.

Step-by-step explanation:

In Part A, the right Riemann sum estimate is calculated using the formula:

`\[ \text{Right Riemann Sum} = \sum_(i=1)^(n) f(x_i) \cdot \Delta x_i \]`

where ( n ) is the number of subintervals,
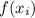`\( f(x_i) \)` is the function value at the right endpoint of the
`\( i \)th` subinterval, and
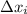`\( \Delta x_i \)` is the width of the
`\( i \)th` subinterval. The calculation involves multiplying the function values by the respective subinterval widths and summing up these products.

In Part B, the midpoint Riemann sum estimate is calculated using the formula:

`\[ \text{Midpoint Riemann Sum} = \sum_(i=1)^(n) f(\bar{x}_i) \cdot \Delta x_i \]`

where
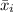`\( \bar{x}_i \)` is the midpoint of the
`\( i \)th` subinterval. The calculation involves evaluating the function at the midpoints, multiplying by the subinterval widths, and summing up these products.

In Part C, the determination of whether the right Riemann sum estimate is an overestimate or underestimate is based on the properties of the function. Since the function is continuously increasing and concave down, the right Riemann sum will be an overestimate. This is because at the right endpoints, the function values contribute more to the sum due to the concavity, leading to an overestimation of the total area under the curve.

Complete Question:

A continuously-increasing function that is concave down on the interval [1, 5] is represented by the table:

2.2

3.1

4.4

5.0

Part A: Find the right Riemann sum estimate of the integral from 1 to 5 of f(x) dx based on the subintervals given in the table: (8 points)

Part B: Write the midpoint Riemann sum that estimates the integral from 1 to 5 of f(x) dx based on the subintervals given in the table: (8 points)

Part C: Determine whether the right Riemann sum estimate is an overestimate or an underestimate based on the properties of the function. (4 points)