Question

Is there a statistically significant difference between the average wait times at these two doctor's offices? Below are 36 randomly selected wait times in minutes from each office. Which of the following are NOT an assumption or condition for this test? Is n big enough? Success/Failure Condition Randomization Assumption Independence Assumption Is there a statistically significant difference between the average wait times at these two doctor's offices? Below are 36 randomly selected wait times in minutes from each office. What is the t stat for this test? Round to two decimal places.

Answer 1

The assumption or condition that is NOT required for this test is the "Success/Failure Condition.

Explanation:

The t-test for comparing the average wait times at two doctor's offices assumes that the data is normally distributed, the samples are independent, and the variances are equal. The "Success/Failure Condition" is not relevant for a t-test, as it is a condition associated with hypothesis tests for proportions. In this case, we are dealing with wait times in minutes, not binary success/failure outcomes.

The t-statistic for this test can be calculated using the formula:

`\[ t = \frac{(\bar{x}_1 - \bar{x}_2)}{\sqrt{(s_1^2)/(n_1) + (s_2^2)/(n_2)}} \]`

where
`\(\bar{x}_1\)` and
`\(\bar{x}_2\)` are the sample means,
`\(s_1\)` and
`\(s_2\)` are the sample standard deviations, and
`\(n_1\)` and
`\(n_2\)` are the sample sizes for the two groups. Substituting the given values into this formula would yield the t-statistic for the test. Ensure that the degrees of freedom are calculated correctly, typically using the formula
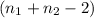`\((n_1 + n_2 - 2)\)` for independent samples.

In conclusion, the "Success/Failure Condition" is not applicable in this context, and the t-statistic can be calculated using the provided formula to assess the statistical significance of the difference in average wait times between the two doctor's offices.