Question

The professor informs the class that there will be a test next week. What is the probability that a randomly selected student studied if they do not pass the test with a b or higher? 0. 45 0. 46 0. 54 0. 59.

Answer 1

The overall probability that a random student gets a B or higher on the test is 0.41 or 41%.

This tree diagram represents a probability tree that can be used to calculate the overall probability of a random student getting a B or higher in the test, considering whether they study or not. To calculate this, we use the law of total probability, which in this context means we sum the probability of studying and getting a B or higher with the probability of not studying and getting a B or higher.

Here are the steps to calculate the overall probability:

1. Probability of Studying and Getting a B or Higher: Multiply the probability that a student studies by the probability that a student gets a B or higher after studying.

2. Probability of Not Studying and Getting a B or Higher: Multiply the probability that a student does not study by the probability that a student gets a B or higher without studying.

3. Total Probability of Getting a B or Higher: Add the two probabilities from the steps above.

Let's calculate each step:

1.
`\( P(\text{Study}) * P(\text{B or higher}|\text{Study}) = 0.6 * 0.55 \)`

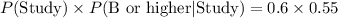
2.
`\( P(\text{Not Study}) * P(\text{B or higher}|\text{Not Study}) = 0.4 * 0.20 \)`

3.
`\( P(\text{B or higher}) = \text{Result from Step 1} + \text{Result from Step 2} \)`

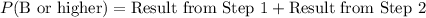
Now, I will perform the calculations.

Here are the step-by-step calculations based on the probabilities given in the tree diagram:

1. Probability of Studying and Getting a B or Higher:

-
`\( P(\text{Study}) * P(\text{B or higher}|\text{Study}) = 0.6 * 0.55 = 0.33 \)`

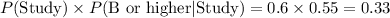
2. Probability of Not Studying and Getting a B or Higher:

-
`\( P(\text{Not Study}) * P(\text{B or higher}|\text{Not Study}) = 0.4 * 0.20 = 0.08 \)`

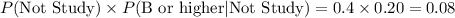
3. Total Probability of Getting a B or Higher:

-
`\( P(\text{B or higher}) = 0.33 + 0.08 = 0.41 \)`

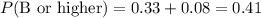
So, the overall probability that a random student gets a B or higher on the test is 0.41 or 41%.

the complete Question is given below:

At the beginning of the semester, a professor tells students that if they study for the tests, then there is a 55% chance they will get a B or higher on the tests. If they do not study, there is a 20% chance that they will get a B or higher on the tests. The professor knows from prior surveys that 60% of students study for the tests. The probabilities are displayed in the tree diagram.