Question

Compare the expressions for the energy stored in an inductor and the energy stored in a capacitor. Select the choices that explain the similarities indicated by the two expressions. Calculating the energy stored in each device involves multiplying by a factor of 1/2. The expressions are equivalent because LC = Δt^2 The proportionality constant used in each expression is determined by the physical properties of the circuit element.

The energy stored in each device is directly proportional to the square of a quantity involving charge. Each device stores an amount of energy that is inverse! The energy stored in each device is directly proportional to a quantity related to current

Answer 1

The expressions for the energy stored in an inductor and a capacitor are similar in several ways, involving multiplying by a factor of 1/2, being directly proportional to current or charge, and determined by the physical properties of the circuit element.

Step-by-step explanation:

The expressions for the energy stored in an inductor and a capacitor are similar in several ways. First, both involve multiplying by a factor of 1/2 when calculating the energy stored in each device. This factor arises from the relationship between the electric field in a capacitor and the magnetic field in an inductor. Second, the expressions for the energy stored in both devices are directly proportional to a quantity related to current or charge, which is represented by L^2 in the case of the inductor and C^2 in the case of the capacitor. Finally, the proportionality constant used in each expression is determined by the physical properties of the circuit element, such as the inductance of the inductor or the capacitance of the capacitor.

Answer 2

The correct statements explaining the similarities indicated by the expressions for the energy stored in an inductor and a capacitor are:

• Calculating the energy stored in each device involves multiplying by a factor of 1/2.
• The energy stored in each device is directly proportional to a quantity related to current.
• The proportionality constant used in each expression is determined by the physical properties of the circuit element.

Why is this correct?

The energy stored in an inductor, given by the equation
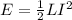`\(E = (1)/(2)LI^2\)`, directly relates to the square of the current passing through it. On the other hand, the energy stored in a capacitor, described by
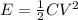`\(E = (1)/(2)CV^2\)`, correlates directly with the square of the voltage across its terminals.

The inductance of an inductor relies on specific physical attributes like the number of wire turns wound around it and the core material used. Similarly, the capacitance of a capacitor is contingent upon physical characteristics such as the size of its plates and the distance separating these plates.

These physical properties ultimately determine how much energy these components can store and the relationships expressed in their respective energy equations.

Question:

Compare the expressions for the energy stored in an inductor and the energy stored in a capacitor. Select the choices that explain the similarities indicated by the two expressions.

1. The expressions are equivalent because =Δ2.

2. Calculating the energy stored in each device involves multiplying by a factor of 1/2.

3. Each device stores an amount of energy that is inversely proportional to the physical dimensions of each device.

4. The energy stored in each device is directly proportional to a quantity related to current.

5. The proportionality constant used in each expression is determined by the physical properties of the circuit element.

6. The energy stored in each device is directly proportional to the square of a quantity involving charge.