Question

an air-track glider of mass m is attached to the end of a horizontal air track by a spring with force constant k as in (figure 1). the air track is turned off, so there is friction between the glider and the track. initially the spring is unstretched, but the glider is initially moving to the left at speed v. the glider moves a distance d to the left before coming momentarily to rest. use the work-energy theorem to find the coefficient of kinetic friction between the glider and the track. express your answer in terms of the variables m , v, k, g, and d.

Answer 1

The coefficient of kinetic friction between the glider and the track can be found using the work-energy theorem. It is given by μ = 2kx^2 / (mgd), where k is the force constant of the spring, x is the initial displacement of the glider, m is the mass of the glider, g is the acceleration due to gravity, and d is the distance travelled by the glider.

Step-by-step explanation:

To find the coefficient of kinetic friction between the glider and the track, we can use the work-energy theorem. The theorem states that the work done on an object is equal to the change in its kinetic energy. In this case, the work done is equal to the initial potential energy of the spring, which is (1/2)kx^2, where x is the initial displacement of the glider. The change in kinetic energy is equal to the work done by friction, which is -μmgd, where μ is the coefficient of kinetic friction, m is the mass of the glider, g is the acceleration due to gravity, and d is the distance travelled by the glider.

Setting the initial potential energy equal to the work done by friction, we get (1/2)kx^2 = -μmgd. Solving for μ, we get:

μ = 2kx^2 / (mgd)

Answer 2

`μ_k = (k * d^2 - ½ * m * v^2) / (m * g * d)`

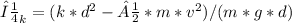
Solving for the Coefficient of Kinetic Friction using Work-Energy Theorem

Figure 1: Air-track glider with spring and friction

Given:

Mass of the glider (m)

Initial velocity of the glider (v)

Spring constant (k)

Acceleration due to gravity (g)

Distance traveled by the glider (d)

To find:

Coefficient of kinetic friction (μ_k)

Approach:

Apply the Work-Energy Theorem:

The work-energy theorem states that the net work done on an object is equal to the change in its kinetic energy. In this case, the net work is done by the spring force and the friction force, and the kinetic energy change is from initial to zero (momentarily at rest).

`W_net = ΔKE`

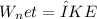
Calculate the Work done by the Spring:

The spring force is conservative, so the work done is equal to the change in potential energy of the spring.

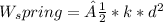`W_spring = ½ * k * d^2` (Since the spring is initially unstretched, the initial potential energy is 0)

Calculate the Work done by Friction:

The friction force is non-conservative, so the work done is equal to the negative of the energy dissipated by friction.

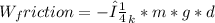`W_friction = -μ_k * m * g * d`(Negative sign indicates energy loss)

Substitute the work expressions and ΔKE:

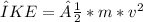`ΔKE = ½ * m * v^2` (Initial kinetic energy)

`½ * k * d^2 - μ_k * m * g * d = ½ * m * v^2`

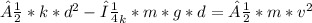
Solve for μ_k:

Rearrange the equation to isolate μ_k:

`μ_k = (k * d^2 - ½ * m * v^2) / (m * g * d)`

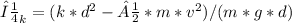
Therefore, the coefficient of kinetic friction (μ_k) can be expressed as:

`μ_k = (k * d^2 - ½ * m * v^2) / (m * g * d)`

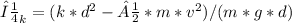
This equation shows that the coefficient of kinetic friction depends on the spring constant, the distance traveled, the initial velocity, the mass of the glider, the acceleration due to gravity, and the distance traveled.