Question

a 45n force is applied to a 5.0 kg object as shown. if the coefficient of friction is 0.55, what is the acceleration of the object

Answer 1

The required value of acceleration is 3.61 m/s².

To find the acceleration of the object, we can use Newton's second law of motion as:

`\[ F_{\text{net}} = m \cdot a \]`

where:

-
`\( F_{\text{net}} \)` is the net force acting on the object,

- m is the mass of the object,

- a is the acceleration.

The net force
`\( F_{\text{net}} \)` is the difference between the applied force
`\( F_{\text{applied}} \)` and the force due to friction
`\( F_{\text{friction}} \)`:

`\[ F_{\text{net}} = F_{\text{applied}} - F_{\text{friction}} \]`

The force due to friction is given by:

`\[ F_{\text{friction}} = \mu \cdot F_{\text{normal}} \]`

where:

-
`\( \mu \)` is the coefficient of friction,

-
`\( F_{\text{normal}} \)` is the normal force.

The normal force is equal to the weight of the object, which is given by
`\( F_{\text{normal}} = m \cdot g \)`

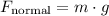
Given:

- Applied force,
`\( F_{\text{applied}} \)` = 45 N

- Mass, m = 5.0 kg

- Coefficient of friction,
`\( \mu \)` = 0.55

- Acceleration due to gravity, g ≈ 9.8 m/s²

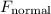`\[ F_{\text{normal}}` = m x g = 5 x 9.8 = 49 N

`F_(friction)` =
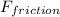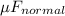`\mu F_(normal)` = 0.55 x 49 = 26.95 N

`\[ F_{\text{net}} = F_{\text{applied}} - F_{\text{friction}} \]` = 45 - 26.95 = 18.05 N

`\[ a = \frac{F_{\text{net}}}{m} \]` =
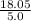`(18.05)/(5.0)` = 3.61 m/s²

The acceleration of the given object is 3.61 m/s².