Question

you are planning a trip in which you go in a spacecraft and travel at a constant velocity for exactly 9 months, as measured by a clock on board the spacecraft, and then return home at the same speed. the overall trip (without stopping) would have felt like 17 years for the people on earth. according to special relativity, how fast must you travel?

Answer 1

The spacecraft must travel at a velocity of approximately 0.9999999967 times the speed of light in order to experience the observed time dilation.

Step-by-step explanation:

According to special relativity, time dilation occurs when an object is moving at a constant velocity relative to an observer. This means that time appears to move slower for the moving object than it does for the observer who is at rest.

Using the given information, we can use the time dilation formula to solve for the velocity required to experience the time dilation observed in this scenario:

t_earth = γ * t_spacecraft

where t_earth is the time elapsed on Earth (17 years), t_spacecraft is the time elapsed on the spacecraft (9 months or 0.75 years), and γ is the Lorentz factor, given by:

γ = 1 /
`\sqrt(1 - v^2/c^2)`

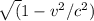
where v is the velocity of the spacecraft, c is the speed of light, and sqrt represents the square root function.

Substituting the given values and solving for v, we get:

17 years = 1 /
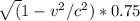`\sqrt(1 - v^2/c^2) * 0.75` years

Multiplying both sides by
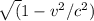`\sqrt(1 - v^2/c^2)` gives:

`\sqrt(1 - v^2/c^2) * 17` = 0.75 years

Squaring both sides and rearranging terms, we get:

`v^2/c^2 = 1 - (0.75/17)^2`

`v/c = \sqrt(1 - (0.75/17)^2)`

`v = c * \sqrt(1 - (0.75/17)^2)`

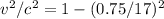
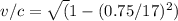
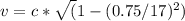
v ≈ 0.9999999967c

Therefore, according to special relativity, the spacecraft must travel at a velocity of approximately 0.9999999967 times the speed of light in order to experience the observed time dilation.