Question

a 2.0-cmcm-tall object is located 8.0 cmcm in front of a converging lens with a focal length of 12.0 cmcm .

Answer 1

The image formed by the converging lens is located 24 cm behind the lens, 6.0 cm tall, inverted, and real.

To determine the location and height of the image formed by a converging lens, we can use the thin lens equation:

`(1)/(f) = (1)/(d_o) + (1)/(d_i)`

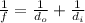
Where:

• f - focal length of the lens
• 
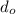  `d_o` - object distance
• 
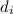  `d_i` - image distance

Given:

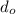`d_o` = 8.0 cm

f = 12.0 cm

By the lens equation,

`(1)/(12) = (1)/(8) + (1)/(d_i)`

`(1)/(d_i)=(1)/(12) - (1)/(8)`

`(1)/(d_i)=(2-3)/(24) = -(1)/(24)`

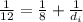
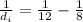
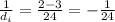
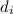`d_i` = -24 cm

The negative sign indicates that the image is formed on the opposite side of the lens from the object, forming an inverted image.

The magnification formula is given by:

m =
`-(d_i)/(d_o)`

m =
`-(-24)/(8)`

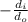
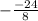
m = 3 cm

Therefore, the image has the height:

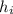`h_i` = 2 (3) = 6 cm

Therefore, the image formed by a converging lens for a 2.0 cm tall object located 8.0 cm away, with a focal length of 12.0 cm, will be 24 cm behind the lens, 6.0 cm tall, inverted, and real.