Question

i have a pool with a rectangular base. the pool's width is two times the depth and its length is three times the depth. i roughly estimate the depth to be 2 m. if my estimate has an error of 5 cm, then use a linear approximation to estimate the maximum volume of water (in cubic meters) i can fit into the pool.

Answer 1

By using a linear approximation based on an estimated depth of 2 m with an error of 5 cm, we find the maximum volume the pool can hold is approximately 55.2 cubic meters (
`m^3`).

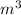Step-by-step explanation:

To estimate the maximum volume of water that can fit into the rectangular pool using linear approximation, we first need to express the pool's dimensions in terms of its depth. Let the depth be represented by d, the width then is 2d, and the length is 3d. The volume V of a rectangular prism is given by the product of its length, width, and depth: V = length × width × depth. Substituting the expressions for the length and width in terms of the depth, we have V = 3d × 2d × d = 6
`d^3`.

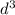If the estimated depth of 2 m has an error of 0.05 m (5 cm), then the maximum possible depth would be d + 0.05 m. We are asked to use linear approximation to estimate the volume, which suggests using the derivative of the volume with respect to depth to find the change in volume. The derivative of V with respect to d is dV/dd = 18
`d^2`. Now we can estimate the change in volume, ΔV, for a small change in depth, Δ1:

ΔV ≈ (dV/dd) × Δd
ΔV ≈ (18×
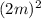`(2 m)^2`) × 0.05 m
ΔV ≈ 36×(4) × 0.05
`m^3`
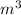
ΔV ≈ 7.2
`m^3`

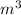
The original volume estimate with a depth of 2 m is V = 6×
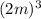`(2 m)^3` = 6× 8
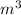`m^3` = 48
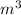`m^3`. Adding our change in volume gives the maximum volume: 55.2
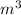`m^3`.

Answer 2

Using linear approximation, the estimated maximum volume for the rectangular pool with a depth error of 5 cm is approximately 51.69 cubic meters.

Step-by-step explanation:

To estimate the maximum volume of a rectangular pool using linear approximation, we assume the given estimates of the pool's dimensions where the pool's width (W) is two times the depth (D) and its length (L) is three times the depth. Given that the estimated depth is 2 meters with a possible error of 5 cm, we express the dimensions as:

• W = 2D
• L = 3D
• D = 2 meters ± 0.05 meters

The volume (V) of the rectangular pool is calculated as:

V = L × W × D

By substituting the relations for L and W in terms of D we get:

V = 3D × 2D × D = 6D^3

Since we are considering the maximum volume, we take the maximum depth to be D = 2.05 m. Hence the estimated maximum volume V_max is:

V_max = 6 × (2.05 m)^3

After calculating, we find that:

V_max = 6 × (2.05)^3 = 6 × 8.615125 m^3 ≈ 51.69075 m^3

The maximum volume of the pool, approximated using linear estimation is approximately 51.69 cubic meters.