The spring must be further compressed by approximately
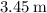 to triple the elastic potential energy.
to triple the elastic potential energy.
The elastic potential energy
 stored in a spring is given by the formula:
stored in a spring is given by the formula:
![\[ U = (1)/(2)kx^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/e95c8hk5e5yrcaxten44cvdaqyxnsdxk8k.png)
where:
-
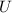 is the elastic potential energy,
is the elastic potential energy,
-
 is the spring constant,
is the spring constant,
-
 is the displacement from the equilibrium position.
is the displacement from the equilibrium position.
In this case, you want to find how much further the spring must be compressed to triple the elastic potential energy. Let
 be the initial displacement (0.26 m), and
be the initial displacement (0.26 m), and
 be the additional displacement.
be the additional displacement.
The elastic potential energy when the spring is compressed by
 is given by:
is given by:
![\[ U_1 = (1)/(2)kx_1^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/44mv6kol45jriop5k83wuu3s7bbqi6n1bi.png)
The elastic potential energy when the spring is further compressed by
 (to triple the energy) is given by:
(to triple the energy) is given by:
![\[ U_2 = (1)/(2)k(x_1 + x_2)^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/x32ojupsavr935b0rk30hhtde2ri43mxnx.png)
Given that
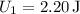 and you want to triple the energy
and you want to triple the energy
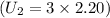 , you can set up the equation:
, you can set up the equation:
![\[ 3 * 2.20 = (1)/(2)k(x_1 + x_2)^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/6in47pdq761dwm9e9gblfut8732dogmtio.png)
Now, substitute the values and solve for
 :
:
![\[ 6.60 = (1)/(2)k(0.26 + x_2)^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/z3chkhu69se0lct1piyu214xvmm4g3zv7y.png)
Multiply both sides by
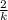 :
:
![\[ 13.20 = (0.26 + x_2)^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/lz0objiv760ar4dnoz3dio6vi7cpiex80m.png)
![\[ 0.26 + x_2 = √(13.20) \]\[ x_2 = √(13.20) - 0.26 \]\[ x_2 \approx 3.45 \, \text{m} \]](https://img.qammunity.org/2024/formulas/physics/high-school/hs6qy3fu6pkr333dcpp3awpmuuucjcwzjy.png)