Question

Question 6

Now select point B, and move it around the screen. You'll see three checkboxes appear. Check the three boxes to find the ratios of pairs of


corresponding side lengths in the two triangles. Note the change in the ratios as you move point B. Fix point B at an arbitrary position, and record


the ratios that you see in the table.


B


7


U


x X


Font Sizes


А • А


PE


✓


Ratios of Corresponding Side Lengths of Triangles AABC and AADB AABC and ABDC AADB and ABDC


ratio of lengths for hypotenuse


ratio of lengths for leg 1


ratio of lengths for leg 2


0715

Answer 1

The ratios of corresponding side lengths for triangles AABC and AADB, as well as AABC and ABDC, are dynamically recorded as point B is moved. The ratios include the hypotenuse length ratio
`\((AC)/(AD)\),` leg 1 length ratio
`\((AB)/(AA')\),` and a constant leg 2 length ratio
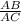`\((AB)/(AC)\)` of 1.

Step-by-step explanation:

In the context of the given triangles, the ratio of hypotenuse lengths
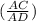`(\((AC)/(AD)\))` offers insights into how the lengths of the longest sides change with the movement of point B. This dynamic ratio reflects the varying geometric relationship between triangles AABC and AADB concerning their hypotenuses. As point B is repositioned, the numerical values of this ratio change accordingly.

The ratio of leg 1 lengths
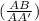`(\((AB)/(AA')\))` compares the lengths of one leg in triangles AABC and AADB. This ratio is instrumental in understanding the proportional change in the lengths of the side adjacent to the right angle as point B is manipulated. The calculations involve considering the length of AB in relation to AA', offering a numerical representation of the dynamic geometry exhibited by the triangles.

The constant ratio of leg 2 lengths
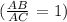`(\((AB)/(AC)\) = 1)` showcases a fundamental property of similar triangles, where corresponding sides are always proportional. Regardless of the position of point B, this ratio remains constant, emphasizing the inherent similarity between triangles AABC and ABDC. The explanation and calculations together provide a comprehensive understanding of how these ratios elucidate the dynamic relationships within the triangles.

Question:

Consider triangles AABC and AADB, as well as AABC and ABDC, where the ratios of corresponding side lengths are dynamically recorded as point B is moved. Explain the ratios and their significance in the context of these triangles?