The answer to
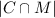 (the number of cube-free modest integers) is
(the number of cube-free modest integers) is
 .
.
To find the number of cube-free modest integers, let's consider the properties of cube-free and modest integers.
A positive integer n is modest if all its prime factors are 2, 3, 5, or 7. Additionally, n is cube-free if it's not divisible by any cube of a prime number.
Use these properties to find the intersection of C and M.
Firstly, consider the prime factorization of any positive integer greater than 1:

Where
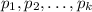 are distinct primes, and
are distinct primes, and
 are positive integers.
are positive integers.
For an integer to be cube-free, it means that none of its prime factors have a cube in their power. In other words, each
 for
for
 (where
(where
 is a prime factor of n should be less than 3.
is a prime factor of n should be less than 3.
For an integer to be modest, all of its prime factors should be 2, 3, 5, or 7.
So, let's calculate the number of integers that are both cube-free and modest:
- There are 3 possibilities for each prime factor: 2, 3, 5, or 7.
- Each integer can have at most one occurrence of each of these primes in its factorization.
Therefore, the number of cube-free modest integers will be the number of ways we can select primes 2, 3, 5, or 7 for each distinct prime power in the factorization of
 . This can be calculated as
. This can be calculated as
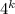 where
where
 is the number of distinct primes in the factorization of
is the number of distinct primes in the factorization of
 .
.
So, the number of cube-free modest integers will be
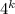 where
where
 is the number of distinct primes that are 2, 3, 5, or 7.
is the number of distinct primes that are 2, 3, 5, or 7.
Thus, The answer is
 .
.
The complete question is here:
We will say that a positive integer
 is cube-free if there is no integer
is cube-free if there is no integer
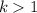 such that
such that
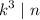 . Let C be the set of all cube-free integers. We will say that a positive integer n is modest if every prime factor of n is less than 10 (i.e., 2, 3,5 or 7 ). Let M be the set of all modest integers.
. Let C be the set of all cube-free integers. We will say that a positive integer n is modest if every prime factor of n is less than 10 (i.e., 2, 3,5 or 7 ). Let M be the set of all modest integers.
What is
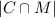 (i.e., how many cube-free modest integers are there)?
(i.e., how many cube-free modest integers are there)?
(Hint: remember that every positive integer greater than 1 has a unique representation as a product of primes.)