Question

use the normal distribution to approximate the following binomial distribution. you claim that 73% of the voters in your district will vote for you. if the district has 350 voters, what is the probability that at least 274 will actually vote for you? a) exam image b) exam image c) exam image d) exam image e) exam image f) none of the above.

Answer 1

The correct option is e.

The probability that at least 274 will actually vote for you is 0.0281

To approximate a binomial distribution using a normal distribution, you can use the mean
`(\(\mu\))` and standard deviation
`(\(\sigma\))` of the binomial distribution. For a binomial distribution with parameters
`\(n\)` (number of trials) and
`\(p\)` (probability of success), the mean is given by
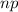`\(np\)` and the standard deviation by
`\(√(np(1-p))\)`.

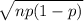Given:

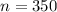`\(n = 350\)` (number of voters)

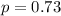`\(p = 0.73\)` (probability of a voter voting for you)

First, find the mean and standard deviation:

`\(\mu = np = 350 * 0.73 = 255.5\)`

`\(\sigma = √(np(1-p)) = √(350 * 0.73 * (1-0.73)) \approx 9.732\)`

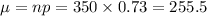
To find the probability that at least 274 voters will vote for you, you can use the normal distribution. Convert this into a z-score:

`\(z = (X - \mu)/(\sigma) = (274 - 255.5)/(9.732) \approx 1.900\)`

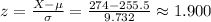
Now, find the probability using the standard normal distribution table or a calculator. The probability of
`\(Z \geq 1.900\)` is approximately
`\(0.0281\)`.

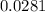Therefore, The answer is 0.0281

Use the normal distribution to approximate the following binomial distribution. You claim that 73% of the voters in your district will vote for you. If the district has 350 voters, what is the probability that at least 274 will actually vote for you?

A. 0.9772

B. 0.0113

C. 0.9890

D. 0.0110

E. 0.0281