The simple pendulum will have a period which is
 times the period on Earth on plant x.
times the period on Earth on plant x.
The formula for period T of a simple pendulum is:
![\[ T = 2\pi \sqrt{(L)/(g)} \]](https://img.qammunity.org/2024/formulas/physics/college/hqdz8737gkt9rj6q11lqv510dv5blsxssc.png)
where:
T - time
L - length of the pendulum,
g - acceleration due to gravity
If the acceleration due to gravity on planet X is three times that on Earth
 , and the length of the pendulum remains the same, we can compare the periods on Earth
, and the length of the pendulum remains the same, we can compare the periods on Earth
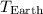 and on planet x
and on planet x
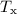 :
:
![\[ T_{\text{x}} = 2\pi \sqrt{\frac{L}{g_{\text{x}}}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/tf7u3i3crgyjddp8dho3pgpqnjkllrnn9m.png)
Substituting
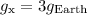 :
:
![\[ T_{\text{x}} = 2\pi \sqrt{\frac{L}{3g_{\text{Earth}}}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/11qxvxskfqysqplymb5hv2u4cte5j2guil.png)
Comparing with the equation for time on Earth,
![\[ \frac{T_{\text{x}}}{T_{\text{Earth}}} = \frac{2\pi \sqrt{\frac{L}{3g_{\text{Earth}}}}}{2\pi \sqrt{\frac{L}{g_{\text{Earth}}}}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/7wzi7zg600ctnb0hectuycr5eazxjbcf0p.png)
![\[ \frac{T_{\text{x}}}{T_{\text{Earth}}} = \sqrt{\frac{g_{\text{Earth}}}{3g_{\text{Earth}}}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/pta4ryp91vw0ep62q9u9rnqjvucgf8zz11.png)
![\[ \frac{T_{\text{x}}}{T_{\text{Earth}}} = \sqrt{(1)/(3)} \]](https://img.qammunity.org/2024/formulas/physics/high-school/pfztef7h8fvjt0v3xbrpnfrx8i1tp1308z.png)
![\[ T_{\text{x}} = (1)/(√(3) )} \cdot T_{\text{Earth}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/q58ozq19xq8ctapg4c8lvs4ove6o8qk4l2.png)
So, the period of the simple pendulum on planet x would be
 times the period on Earth.
times the period on Earth.