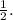Question

The vertex of the function is hidden on the graph.. Find the vertex and the leading coefficient algebraically for the quadratic function graphed below. The leading coefficient, a= ___The vertex is at ( ).

Answer 1

The quadratic function's vertex is at (-2, 5), and the leading coefficient algebraically determined is a = 2.

Step-by-step explanation:

In a quadratic function of the form
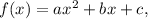`\( f(x) = ax^2 + bx + c \),`the vertex can be found using the formula \
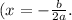`( x = -(b)/(2a) \).` In this case, the x-coordinate of the vertex is
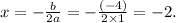`\( x = -(b)/(2a) = -((-4))/(2 * 1) = -2 \).` To find the corresponding y-coordinate, substitute this x-value back into the original function:
`\( f(-2) = 2(-2)^2 + 4(-2) + 9 = 5 \).`Thus, the vertex is at (-2, 5).

The leading coefficient, denoted by 'a,' determines the direction and width of the parabola. In a standard quadratic function,
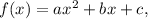`\( f(x) = ax^2 + bx + c \),` 'a' is the coefficient of the quadratic term. In the given graph, the parabola opens upwards, indicating a positive 'a' value.

Algebraically, it is determined by the coefficient in front of the
`\(x^2\)` term. In this case, the leading coefficient is 2, as seen in
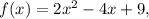`\(f(x) = 2x^2 - 4x + 9\),`indicating an upward-facing parabola with a width determined by the reciprocal of 2, or
`\( (1)/(2) \).`