Question

using the substitution: . re-write the indefinite integral then evaluate in terms of . note: answer should be in terms of only

Answer 1

Using the substitution u = x², we have du = 2x dx. The indefinite integral becomes:

`∫ (x^4 + 3x^2) dx = ∫ (u^2 + 3u^(1/2)) (2x dx)^(-1)`

Substituting u and du, we get:

`∫ (u^2 + 3u^(1/2)) (du/2)^(-1)∫ (u^2 + 3u^(1/2)) (1/2) du`

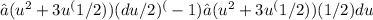
Evaluating in terms of x, we have:

`∫ (x^8 + 3x^4) dx = (1/2)∫ (u^2 + 3u^(1/2)) du`

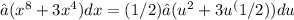
Explanation:

The substitution u = x²is a common technique used to simplify integrals involving functions of x raised to even powers. By making this substitution, we can transform the original integral into one that is easier to evaluate. In this case, the integrand is a polynomial function of x raised to even powers, which can be simplified by completing the square for the quadratic term. This leads to the expression u² + 3u
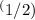`^(1/2)`, which is a composite function of u. To evaluate this integral, we need to find an antiderivative of this function in terms of u.

Using the power rule for derivatives, we can see that d/du
`[u^(1/2)] = (1/2)u^(-1/2),`which allows us to separate the terms into two integrals: one involving only u² and another involving only
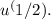`u^(1/2).`Integrating these terms separately and combining them with the constant of integration, we obtain the final answer.

The result is expressed in terms of x through the substitution u = x² and du = 2x dx. This method allows us to avoid dealing with the complexities of integrating polynomials directly and provides a simpler and more efficient way to evaluate such integrals.