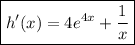Answer:
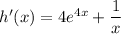
Explanation:
Given the function:
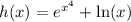
we can find its derivative using:
- the sum/difference rule ...
![\left[\frac{}{}f(x) \pm g(x)\frac{}{}\right]' = f'(x) \pm g'(x)](https://img.qammunity.org/2024/formulas/mathematics/college/577o911sou59kvrhbawyq1proj7zt9qjtd.png)
- the chain rule ...
![\left[\frac{}{}f(x)^n\frac{}{}\right]' = n \left[\frac{}{}f(x)\frac{}{}\right]^(n\,-\,1) \cdot f'(x)](https://img.qammunity.org/2024/formulas/mathematics/college/zapun8e1kqr9rackgy1tzl3gf746dlej2l.png)
- the common derivatives ...
![\left[\,e^x\,\right]' = e^x](https://img.qammunity.org/2024/formulas/mathematics/college/epdxxvav7fjlyrg1x4u7y3xnfongpp4mga.png) ...
...
![\left[\frac{}{}\ln(x)\frac{}{}\right]' = (1)/(x)](https://img.qammunity.org/2024/formulas/mathematics/college/u0ytckr2dulv2d2q5fc0od1bpx87zbe6l0.png)
First, we can apply the sum/difference rule.
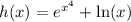
![h'(x) = \left[\frac{}{}e^(x^4)\frac{}{}\right]' + \left[\frac{}{}\ln(x)\frac{}{}\right]'](https://img.qammunity.org/2024/formulas/mathematics/college/w9o6pfri8e0hyrfqj0tjbq19qf8zbuzt3x.png)
Next, we can simplify the derivative of
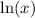 .
.
![h'(x) = \left[\frac{}{}e^(x^4)\frac{}{}\right]' + (1)/(x)](https://img.qammunity.org/2024/formulas/mathematics/college/kty3wlc8ak8chzfd35g50qz9dyg3e4jqkb.png)
Then, we can simplify the derivative of the first term using the chain rule.
![h'(x) = \left[\frac{}{}4\,[\,e^x\,]^((4\, -\, 1))\cdot e^x\frac{}{}\right] + (1)/(x)](https://img.qammunity.org/2024/formulas/mathematics/college/9twx9ejz06rfc1alomfad6nrslassk13jd.png)
Finally, this can be simplified using the properties of exponents.