Question

A space shuttle astronaut in a circular orbit around the Earth has an assembly consisting of two small dense spheres, each of mass m, whose centers are connected by a rigid rod of length ℓ and negligible mass. The astronaut also has a device that will launch a small lump of clay of mass m at speed v0, Express your answers in terms of m, v0, ℓ , and fundamental constants

Answer 1

In this scenario, a space shuttle astronaut has an assembly consisting of two small spheres connected by a rigid rod. The gravitational force between the spheres and their initial acceleration can be calculated using Newton's laws of universal gravitation and motion.

Step-by-step explanation:

In this scenario, the assembly consists of two small spheres with a mass of m each, connected by a rigid rod of length ℓ and negligible mass. The astronaut has a device that can launch a small lump of clay with mass m at speed v0.

Since the space shuttle is in a circular orbit around the Earth, gravity provides the necessary centripetal force to keep the assembly in motion. The gravitational force between the two spheres can be calculated using Newton's law of universal gravitation:

F = G * (m * m) / r2

where G is the gravitational constant and r is the distance between the centers of the spheres.

The initial acceleration of the assembly can be calculated using Newton's second law:

a = F / (2m)

where F is the gravitational force between the spheres and 2m is the total mass of the assembly.

Answer 2

The total kinetic energy of the system after collision is
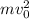`\(m v_0^2\)`, and the change in kinetic energy after collision is also
`\(m v_0^2\)`.

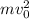Given:

Initially, the assembly is freely floating at rest relative to the cabin, and the astronaut launches the clay lump in such a way that it perpendicularly strikes and sticks to the rod's midpoint.

The system consists of two small dense spheres connected by a rigid rod, and the entire assembly is in a circular orbit around the Earth. The system is at rest, and then a lump of clay of mass m is launched at speed
`\(v_0\)`. After the collision, the system will have a new configuration, and we need to find the total kinetic energy of the system and the change in kinetic energy.

Let's denote the mass of each small dense sphere as \(m\), the length of the rod as l, and the speed of the clay lump as
`\(v_0\)`.

• Rotational Kinetic Energy (after the collision):

The two small spheres and the rod will now be rotating about the center of mass of the system. The moment of inertia (
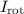`\(I_{\text{rot}}\)`) for a system of two point masses rotating about an axis passing through the center of mass is given by:

`\[ I_{\text{rot}} = 2 * m * \left((l)/(2)\right)^2 \]`

The rotational kinetic energy (\(KE_{\text{rot}}\)) is given by:

`\[ KE_{\text{rot}} = (1)/(2) I_{\text{rot}} \omega^2 \]`

where
`\(\omega\)` is the angular velocity.

`\[ \omega = (v_0)/((l)/(2)) = (2v_0)/(l) \]`

`\[ KE_{\text{rot}} = (1)/(2) \left((1)/(2) m l^2\right) \left((2v_0)/(l)\right)^2 = (1)/(2) m v_0^2 \]`

• Linear Kinetic Energy of the Clay Lump (after the collision):

The linear kinetic energy (
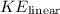`\(KE_{\text{linear}}\)`) of the clay lump is given by:

`\[ KE_{\text{linear}} = (1)/(2) m v_0^2 \]`

The total kinetic energy,
`\(KE_{\text{total}}\)` =
`mv_(0)^(2)`

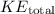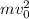
The change in kinetic energy is the difference between the total kinetic energy after the collision and the initial total kinetic energy.

`\[ \Delta KE = KE_{\text{total}} - KE_{\text{initial}} \]`

Given the system is initially at rest, the initial kinetic energy is zero. Therefore, the change in kinetic energy is equal to the total kinetic energy after the collision:

`\[ \Delta KE = KE_{\text{total}} = m v_0^2 \]`

So, the total kinetic energy of the system after the collision is
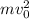`\(m v_0^2\)`, and the change in kinetic energy is also
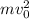`\(m v_0^2\)`.