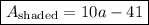Question

PLEASE HELP ME I NEED HELP!!!!!!!!!!!!!!

Answer 1

`10a - 41`

Explanation:

We can represent the area of the shaded section with the equation:

`A_\text{shaded} = A_\text{rect} - A_\text{square}`

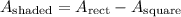
First, we can solve for the area of the large enclosing rectangle:

`A_\text{rect} = l \cdot w`

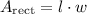
↓ plugging in the given side lengths

`A_\text{rect} = (a+4)(a-4)`

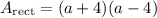
↓ applying the difference of squares formula ...
`(a + b)(a - b) = a^2 - b^2`

`A_\text{rect} = a^2 - 16`

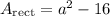
Next, we can find the area of the non-shaded square.

`A_\text{square} = l^2`

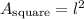
↓ plugging in the given side length

`A_\text{square} = (a-5)^2`

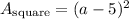
↓ applying the binomial square formula ...
`(a - b)^2 = a^2 - 2b + b^2`

`A_\text{square} = a^2 - 10a + 25`

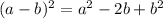
Finally, we can plug these areas into the equation for the area of the shaded section.

`A_\text{shaded} = A_\text{rect} - A_\text{square}`

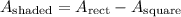
↓ plugging in the areas we solved for

`A_\text{shaded} = \left[\frac{}{}a^2 - 16\frac{}{}\right] - \left[\frac{}{}a^2 - 10a + 25\frac{}{}\right]`

↓ distributing the negative to the subterms within the second term

`A_\text{shaded} = \left[\frac{}{}a^2 - 16\frac{}{}\right] + \left[\frac{}{}-a^2 + 10a - 25\frac{}{}\right]`

↓ applying the associative property

`A_\text{shaded} = a^2 - 16 -a^2 + 10a - 25`

↓ grouping like terms

`A_\text{shaded} = (a^2 -a^2) + 10a + (- 16 - 25)`

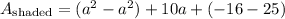
↓ combining like terms

`\boxed{A_\text{shaded} = 10a - 41}`