Question

Normal conversation has a sound level of about 60 dB. How many times more intense must a 10,000-Hz sound be compared to a 1000-Hz sound to be perceived as equal to 60 phons of loudness

Answer 1

Answer: A 10,000-Hz sound is 10 times more intense as compared to a 1000-Hz sound to be perceived as equal to 60 phons of loudness.

Step-by-step explanation:

The formula used is as follows.

`\beta = 10 dB log ((I)/(I_(o)))\\60 = 10 dB log ((I)/(I_(o)))`

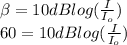
`I_(o) = 10^(-12)` normal threshold

The difference is sound level is as follows.

60 - 60 = 0

Hence,

`0 = 10 dB [log ((I_(f))/(I_(o))) - log ((I_(i))/(I_(o)))]\\log ((1000)/(I_(o))) = log ((10000 x)/(I_(o)))\\log (10^(15)) = log (10^(16)x)\\15 = 16 + log x\\log x = 1\\x = 10`

This means that 10,000 Hz sound is 10 times more intense.

Thus, we can conclude that a 10,000-Hz sound is 10 times more intense as compared to a 1000-Hz sound to be perceived as equal to 60 phons of loudness.