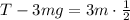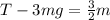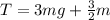Question

a yo-yo is constructed of three disks: two outer disks of mass m, radius r and thickness d, and an inner disk of mass m, radius r and thickness d. the yo-yo is suspended from the ceiling and then released with the string vertical. calculate the tension in the string as the yo-yo falls. note that when the center of the yo-yo moves down a distance y, the yo-yo turns through an angle y/r, which in turn means that the angular speed w is equal to vcm/4

Answer 1

The tension in the string as the yo-yo falls can be calculated using the principles of rotational motion. The tension provides the centripetal force needed to keep the yo-yo rotating without slipping. The formula to calculate tension is T = (1/2 * m * r^2) * (a/r).

Step-by-step explanation:

The tension in the string as the yo-yo falls can be calculated using the principles of rotational motion. The tension in the string provides the centripetal force needed to keep the yo-yo rotating without slipping. It can be calculated using the equation T = I * alpha, where T is the tension, I is the moment of inertia, and alpha is the angular acceleration.

In this case, the yo-yo can be considered as a solid cylinder with mass m and radius r. The moment of inertia of a solid cylinder rotating about its axis is given by I = 1/2 * m * r^2. The angular acceleration can be calculated using alpha = a/r, where a is the linear acceleration of the yo-yo.

Therefore, the tension in the string is T = (1/2 * m * r^2) * (a/r) = 1/2 * m * a * r.

Answer 2

The tension in the string as the yo-yo falls is
`\(T = 3mg + (3)/(2)m\)`.

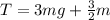The tension in the string can be calculated by considering the forces and motions involved as the yo-yo falls.

First, let's determine the relationship between the linear speed
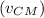`(\(v_(CM)\))` and the angular speed
`(\(\omega\))` of the yo-yo:

`\(\omega = (v_(CM))/(r)\)`

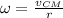
where r is the radius of the yo-yo.

Given that the center of the yo-yo moves down a distance y and the yo-yo turns through an angle y/r, we can relate linear speed to angular speed.

`\(v_(CM) = \omega \cdot r = (y)/(r) \cdot r = y\)`

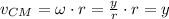
Now, let's consider the forces involved. The tension in the string (T) provides the force necessary to accelerate the yo-yo downward and also generates the torque for rotation.

The net force accelerating the yo-yo downward is the difference between the tension and the gravitational force:

`\(T - 3mg = 3ma\)`

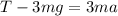
where:

m = mass of each disk

g = acceleration due to gravity

a = acceleration of the yo-yo's center of mass

The factor of
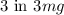`\(3\) in \(3mg\)` accounts for the gravitational force acting on the three disks (two outer disks and the inner disk).

The linear acceleration of the yo-yo's center of mass (a) can be related to the linear speed
`(\(v_(CM)\))`:

`\(a = \frac{{dv_(CM)}}{{dt}} = \frac{{dy}}{{dt}} = v_(CM) \cdot \frac{{dy}}{{dt}} = y \cdot \frac{{dy}}{{dt}}\)`

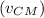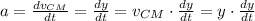
Using the chain rule:
`\(\frac{{dy}}{{dt}} = v_(CM)\)`

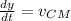
Now, we know that
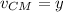`\(v_(CM) = y\)`, so:

`\(\frac{{dy}}{{dt}} = y\)`

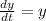
This is a differential equation, and to solve it, we'll separate variables and integrate:

`\(\int y \, dy = \int dt\)`

Integrating both sides:

`\(\frac{{y^2}}{2} = t + C\)`

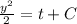
Where C is the constant of integration. Considering the initial condition that at t = 0, y = 0 (when the yo-yo is released), we find that C = 0.

So, we get:

`\(\frac{{y^2}}{2} = t\)`

Now, differentiating both sides with respect to
`\(t\) to find \(a = \frac{{dy}}{{dt}}\)`:

`\(y \cdot \frac{{dy}}{{dt}} = 2 \cdot \frac{{dy}}{{dt}} = 1\)`

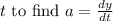This means
`\(a = (1)/(2)\)`.

Now, going back to our force equation:

`\(T - 3mg = 3ma\)`

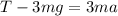
Substitute
`\(a = (1)/(2)\)` and rearrange:

`\(T - 3mg = 3m \cdot (1)/(2)\)`

`\(T - 3mg = (3)/(2)m\)`

`\(T = 3mg + (3)/(2)m\)`