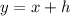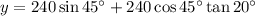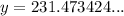Question

!50 POINTS! (2 SIMPLE GEOMETRY QUESTIONS)

QUESTIONS BELOW
|
|
\/

Answer 1

`\begin{aligned}\textsf{1)}\;\;x &= 219.2 \; \sf ft\\y &= 299.0\; \sf ft\\z&= 219.2\; \sf ft\end{aligned}`

`\begin{aligned}\textsf{2)}\;\;x&=169.7\; \sf ft\\y&= 231.5\; \sf ft\\z&= 169.7\; \sf ft\end{aligned}`

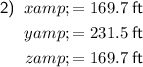
Explanation:

Question 1

The given diagram shows a right triangle, with height x, and base z. The angle of depression is 45°, and the hypotenuse of the triangle is 310 feet.

To determine the values of x and z, we can use trigonometric ratios.

`\boxed{\begin{minipage}{9.4 cm}\underline{Trigonometric ratios} \\\\$\sf \sin(\theta)=(O)/(H)\quad\cos(\theta)=(A)/(H)\quad\tan(\theta)=(O)/(A)$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf O$ is the side opposite the angle. \\\phantom{ww}$\bullet$ $\sf A$ is the side adjacent the angle. \\\phantom{ww}$\bullet$ $\sf H$ is the hypotenuse (the side opposite the right angle). \\\end{minipage}}`

The values of the right triangle are:

• θ = 45°
• O = x
• A = z
• H = 310 ft

To find the value of x, use the sine ratio:

`\sin 45^(\circ)=(x)/(310)`

`x=310 \sin 45^(\circ)`

`x=219.203102...`

`\boxed{\boxed{x=219.2\; \sf ft}}`

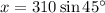
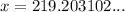
To find the value of z, use the cosine ratio:

`\cos 45^(\circ)=(z)/(310)`

`z=310 \cos 45^(\circ)`

`z=219.203102...`

`\boxed{\boxed{z=219.2\; \sf ft}}`

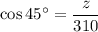
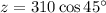
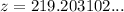
The value of y is the sum of x and the height of the smaller right triangle (with base z and angle of elevation of 20°).

Let "h" be the height of the smaller right triangle. Therefore, the values of the smaller right triangle are:

• θ = 20°
• O = h
• A = z = 310 cos 45°

To find an expression for the height of the smaller right triangle, use the tangent ratio:

`\tan 20^(\circ)=(h)/(z)`

`\tan 20^(\circ)=(h)/(310 \cos 45^(\circ))`

`h=310 \cos 45^(\circ)\tan 20^(\circ)`

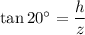
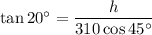
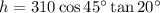
Therefore, the value of y is:

`y = x + h`

`y = 310 \sin 45^(\circ) + 310 \cos 45^(\circ)\tan 20^(\circ)`

`y=298.986506...`

`\boxed{\boxed{y=299.0\; \sf ft}}`

`\hrulefill`

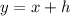
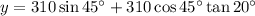
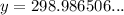
Question 2

This question is exactly the same as question 1, with the exception of the hypotenuse of the larger triangle now being 240 feet. Therefore, we can use the same method as question 1 to find the values of x, y and z. All we need to do is substitute H = 240 into the calculations.

The values of the right triangle are:

• θ = 45°
• O = x
• A = z
• H = 240 ft

To find the value of x, use the sine ratio:

`\sin 45^(\circ)=(x)/(240)`

`x=240 \sin 45^(\circ)`

`x=169.705627...`

`\boxed{\boxed{x=169.7\; \sf ft}}`

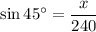
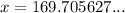
To find the value of z, use the cosine ratio:

`\cos 45^(\circ)=(z)/(240)`

`z=240 \cos 45^(\circ)`

`z=169.705627...`

`\boxed{\boxed{z=169.7\; \sf ft}}`

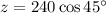
The value of y is the sum of x and the height of the smaller right triangle (with base z and angle of elevation of 20°).

Let "h" be the height of the smaller right triangle. Therefore, the values of the smaller right triangle are:

• θ = 20°
• O = h
• A = z = 240 cos 45°

To find an expression for the height of the smaller right triangle, use the tangent ratio:

`\tan 20^(\circ)=(h)/(z)`

`\tan 20^(\circ)=(h)/(240 \cos 45^(\circ))`

`h=240 \cos 45^(\circ)\tan 20^(\circ)`

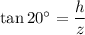
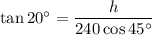
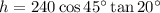
Therefore, the value of y is:

`y = x + h`

`y = 240\sin 45^(\circ) + 240\cos 45^(\circ)\tan 20^(\circ)`

`y=231.473424...`

`\boxed{\boxed{y=231.5\; \sf ft}}`