Question

(100 POINTS!!!) The polynomial function

M(t)= 0.5t^4 + 3.45t^3 -96.65t^2 +347.7t
can be used to estimate the number of milligrams of the pain relief medication ibuprofen in the bloodstream t hours after 400 mg of the medication has been taken. Find the number of milligrams of ibuprofen in the bloodstream at t = 0, 1, 2, and so on, up to 6 hr.

Round the function values to the nearest tenth.

Then Use the function values you found in the previous question to sketch a graph of the function.

Answer 1

See attached

Explanation:

`M(t)= 0.5t^4 + 3.45t^3 -96.65t^2 +347.7t`

for t = 0, 1, 2, 3, 4, 5 and 6

`M(0)= 0.5(0^4) + 3.45(0^3) -96.65(0^2) +347.7(0) = 0\\\\M(1)= 0.5(1^4) + 3.45(1^3) -96.65(1^2) +347.7(1) =255\\\\M(2) = 0.5(2^4) + 3.45(2^3) -96.65(2^2) +347.7(2)=344.4\\\\M(3)= 0.5(3^4) + 3.45(3^3) -96.65(3^2) +347.7(3) =306.9\\\\M(4)= 0.5(4^4) + 3.45(4^3) -96.65(4^2) +347.7(4)=193.2\\\\M(5)= 0.5(5^4) + 3.45(5^3) -96.65(5^2) +347.7(5)=66\\\\M(6)= 0.5(6^4) + 3.45(6^3) -96.65(6^2) +347.7(6)=0\\`

Plotting M(t) against t we will get the graph

Answer 2

`\begin{array}ct&M(t)\\\cline{1-2} 0&0\\1&255\\2&344.4\\3&306.9\\4&193.2\\5&66\\6&0\end{array}`

See attached for the graph of the function.

Explanation:

Given polynomial function:

`M(t)= 0.5t^4 + 3.45t^3 -96.65t^2 +347.7t`

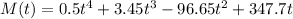
The given polynomial function can be used to estimate the number of milligrams of the pain relief medication ibuprofen in the bloodstream t hours after 400 mg of the medication has been taken.

To find the number of milligrams of ibuprofen in the bloodstream at different time points, substitute the given values of t into the given function M(t).

`\begin{aligned}t=0 \implies M(0)&= 0.5(0)^4 + 3.45(0)^3 -96.65(0)^2 +347.7(0)\\&=0+0+0+0\\&=0\; \sf mg\end{aligned}`

`\begin{aligned}t=1 \implies M(1)&= 0.5(1)^4 + 3.45(1)^3 -96.65(1)^2 +347.7(1)\\&=0.5(1)+ 3.45(1) -96.65(1) +347.7(1)\\&=0.5 + 3.45 -96.65 +347.7\\&=255\; \sf mg\end{aligned}`

`\begin{aligned}t=2 \implies M(2)&= 0.5(2)^4 + 3.45(2)^3 -96.65(2)^2 +347.7(2)\\&= 0.5(16) + 3.45(8) -96.65(4) +347.7(2)\\&=8+27.6-386.6+695.4\\&=344.4\; \sf mg\end{aligned}`

`\begin{aligned}t=3 \implies M(3)&= 0.5(3)^4 + 3.45(3)^3 -96.65(3)^2 +347.7(3)\\&= 0.5(81) + 3.45(27) -96.65(9) +347.7(3)\\&=40.5+93.15-869.85+1043.1\\&=306.9 \; \sf mg\end{aligned}`

`\begin{aligned}t=4 \implies M(4)&= 0.5(4)^4 + 3.45(4)^3 -96.65(4)^2 +347.7(4)\\&= 0.5(256) + 3.45(64) -96.65(16) +347.7(4)\\&=128+220.8-1546.4+1390.8\\&=193.2\; \sf mg\end{aligned}`

`\begin{aligned}t=5 \implies M(5)&= 0.5(5)^4 + 3.45(5)^3 -96.65(5)^2 +347.7(5)\\&= 0.5(625) + 3.45(125) -96.65(25) +347.7(5)\\&=312.5+431.25-2416.25+1738.5\\&=66\; \sf mg\end{aligned}`

`\begin{aligned}t=6 \implies M(6)&= 0.5(6)^4 + 3.45(6)^3 -96.65(6)^2 +347.7(6)\\&= 0.5(1296) + 3.45(216) -96.65(36) +347.7(6)\\&=648+745.2-3479.4+2086.2\\&=0\; \sf mg\end{aligned}`

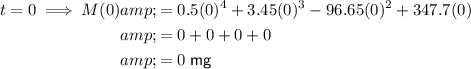
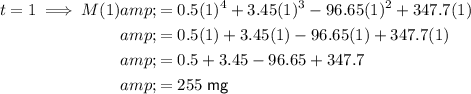
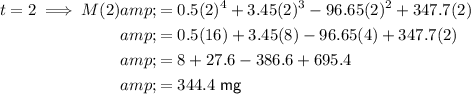
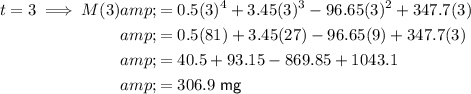
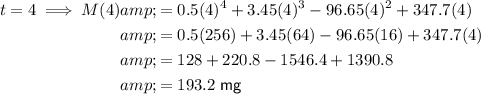
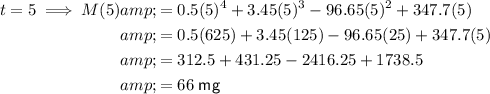
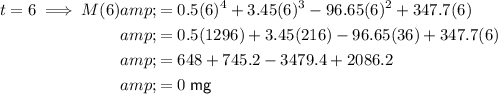
To sketch a graph of the function, plot these values on a graph with time on the x-axis and ibuprofen concentration on the y-axis, and draw a smooth curve through the plotted points. An appropriate scale to use is x-axis : y-axis = 1 : 50.