Question

!50 POINTS! (3 SIMPLE GEOMETRY QUESTIONS)

QUESTIONS BELOW
|
|
\/

Answer 1

1) 1388.1

2) x = 176.8

z = 176.8

y = 241.1

3) x = 205.1

z = 205.1

y = 279.7

Explanation:

`sin(\theta) = (opp)/(hyp) \\\\cos(\theta) = (adj)/(hyp) \\\\tan(\theta) = (opp)/(adj)`

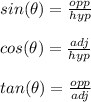
1)

x = 1046

∠A = 53

tan A = h/x

h = x * tanA

h = 1046*tan(53)

=1388.1

2)

Since AD is the horizontal tine, it is parallel to BC

⇒ ∠BAD = 90

⇒ ∠BAC + ∠CAD = 90

⇒ ∠BAC + 45 = 90

⇒ ∠BAC = 90 - 45

⇒ ∠BAC = 45

In ΔABC,

∠BAC + ∠ABC + ∠ACB = 180

45 + 90 + ∠ACB = 180

∠ACB = 45

Since ∠ACB = ∠BAC, the sides opposite to these angle are equal

⇒ x = z

By pythagorean theorem

x² + z² = 250²

⇒ x² + x² = 250²

⇒ 2x² = 250²

⇒ x² = 250²/2

⇒ x = √[250²/2]

⇒ x = 250/√(2)

⇒ x = 176.8

⇒ z = 176.8

In Δ AED,

AD = z

∠EAD = 20

⇒ tan(EAD) = DE/AD

⇒ DE = AD * tan(EAD)

⇒ DE = z * tan(20)

y = CD + DE

⇒ y = x + z *tan(20)

⇒ y = x + x *tan(20)

⇒ y = x (1 + tan(20))

⇒ y = 250 (1 + tan(20))/√(2)

⇒ y = 241.1

3) Since AD is the horizontal tine, it is parallel to BC

⇒ ∠BAD = 90

⇒ ∠BAC + ∠CAD = 90

⇒ ∠BAC + 45 = 90

⇒ ∠BAC = 90 - 45

⇒ ∠BAC = 45

In ΔABC,

∠BAC + ∠ABC + ∠ACB = 180

45 + 90 + ∠ACB = 180

∠ACB = 45

Since ∠ACB = ∠BAC, the sides opposite to these angle are equal

⇒ x = z

By pythagorean theorem

x² + z² = 290²

⇒ x² + x² = 290²

⇒ 2x² = 290²

⇒ x² = 290²/2

⇒ x = √[290²/2]

⇒ x = 290/√(2)

⇒ x = 205.1

⇒ z = 205.1

In Δ AED,

AD = z

∠EAD = 20

⇒ tan(EAD) = DE/AD

⇒ DE = AD * tan(EAD)

⇒ DE = z * tan(20)

y = CD + DE

⇒ y = x + z *tan(20)

⇒ y = x + x *tan(20)

⇒ y = x (1 + tan(20))

⇒ y = 290 (1 + tan(20))/√(2)

⇒ y = 279.7