Question

!25 POINTS! (1 SIMPLE GEOMETRY QUESTION)

QUESTION BELOW
|
|
\/

Answer 1

x = 162.6

z = 162.6

y = 221.8

Explanation:

Since AD is the horizontal tine, it is parallel to BC

⇒ ∠BAD = 90

⇒ ∠BAC + ∠CAD = 90

⇒ ∠BAC + 45 = 90

⇒ ∠BAC = 90 - 45

⇒ ∠BAC = 45

In ΔABC,

∠BAC + ∠ABC + ∠ACB = 180

45 + 90 + ∠ACB = 180

∠ACB = 45

Since ∠ACB = ∠BAC, the sides opposite to these angle are equal

⇒ x = z

By pythagorean theorem

x² + z² = 230²

⇒ x² + x² = 230²

⇒ 2x² = 230²

⇒ x² = 230²/2

⇒ x = √[230²/2]

⇒ x = 230/√(2)

⇒ x = 162.6

⇒ z = 162.6

In Δ AED,

AD = z

∠EAD = 20

⇒ tan(EAD) = DE/AD

⇒ DE = AD * tan(EAD)

⇒ DE = z * tan(20)

y = CD + DE

⇒ y = x + z *tan(20)

⇒ y = x + x *tan(20)

⇒ y = x (1 + tan(20))

⇒ y = 230 (1 + tan(20))/√(2)

⇒ y = 221.8

Answer 2

• x=162.2 ft
• y=221.8 ft
• z=162.2 ft

Explanation:

Solution:

For Lower left right angled triangle:

It is an isosceles right angled triangle cause one angle is 90-45=45°.

Remaining angle also be 45°

If two angles of triangle are equal than it is an isosceles triangle.

Therefore, x=z.

Pair of corresponding two side of isosceles triangle are equal.

Hypotenuse= 230 ft

We can use Pythagoras formula

`\tt h^2= p^2+b^2\\230^2=x^2+z^2\\230^2=x^2+x^2\\230^2=2x^2\\2x^2=52900\\x^2=(52900)/(2)\\x^2=26450`

`x=√(26450)`

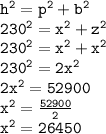
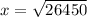
x=162.634 ft

z=162.634 ft

For Upper right right angled triangle:

angle of elevation=20 degree

Adjacent=219.203

Opposite= a let

Now , we have

`\tt Tan \:Angle = (opposite)/(adjacent)`

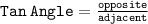
Tan 20=a/162.63456

a=Tan 20*162.63456

a=59.2

Now

Value of y= x+a= 162.63456 ft + 59.2 ft=221.8

Therefore,

x=162.2 ft

y=221.8 ft

z=162.2 ft