Question

!50 POINTS! (3 SIMPLE GEOMETRY QUESTIONS)

QUESTIONS BELOW
|
|
\/

Answer 1

1st picture: x=4.6

2nd picture: 703.5 ft.

3rd picture:

• x=219.2 ft
• y= 298.9 ft
• z=219.2 ft

Explanation:

For 1st picture:

Given:

Angle A= 55°

Adjacent = x =?

Hypotenuse = c=8

If we know the angle, adjacent and hypotenuse in right angled triangle,

we can use :

`\boxed{\tt Cos \:Angle = (Adajcent)/(Hypotenuse)}`

`\tt Cos \:55 = (x)/(8)`

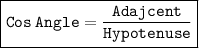
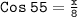
doing Criss cross multiplication

`\tt x= cos 55*8`

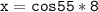
x=4.6

`\hrulefill`

For 2nd picture:

Solution:

From bottom of the flag:

Angle= 41 degree

opposite: 1660 ft

Adjacent: y let

Now using Tan angle formula

`\tt Tan \:Angle = (opposite)/(adjacent)`

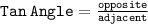
Tan 41= 1660/y

y=1660/Tan(41)

y=1909.6 ft

Again:

From top of the flag:

Angle= 54 degree

opposite: 1660 ft

Adjacent: z let

Now using Tan angle formula

`\tt Tan \:Angle = (opposite)/(adjacent)`

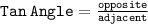
Tan 54= 1660/z

z=\frac{1660}{Tan(54)}

z=1206.1 ft

Now

The height of the flagpole = z-y=1206.1-1909.6= - 703.5

Since length is always positive so height of the flagpole is 703.5 ft.

`\hrulefill`

For 3rd picture:

Solution:

For Lower left right angled triangle:

It is an isosceles right angled triangle cause one angle is 90-45=45°.

Remaining angle also be 45°

If two angles of triangle are equal than it is an isosceles triangle.

Therefore, x=z.

Pair of corresponding two side of isosceles triangle are equal.

Hypotenuse= 310 ft

We can use Pythagoras formula

`\tt h^2= p^2+b^2\\310^2=x^2+z^2\\310^2=x^2+x^2\\310^2=2x^2\\2x^2=96100\\x^2=(96100)/(2)\\x^2=48050`

`x=√(48050)`

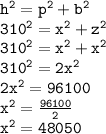
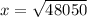
x=219.2 ft

z=219.2 ft

For Upper right right angled triangle:

angle of elevation=20 degree

Adjacent=219.203

Opposite= a let

Now , we have

`\tt Tan \:Angle = (opposite)/(adjacent)`

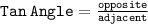
Tan 20=a/219.203

a=Tan 20*219.203

a=79.8

Now

Value of y= x+a=219.203+79.783=298.9 ft