Answer:
y =
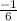 x +
x +
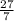
Explanation:
(-1,2) (6,3)
y = mx + b
To write the equation, we need two things. We need the slope (m) and the y-intercept (b). We will use the two points given to do this.
Slope
Slope is the change in y over the change in x. We find the change by subtracting. From the points given, the y values are 3 and 2. From the points give, the x values are 6 and -1
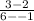 =
=
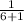 =
=

The slope (m) is

y-intercept
to find the y-intercept we need the slope
 and one of the two points given. It does not matter which point we use. I am going to use (6,3) because I would rather deal with positive numbers
and one of the two points given. It does not matter which point we use. I am going to use (6,3) because I would rather deal with positive numbers
We are going to us the x value of 6 and the y value to 3 and plug it into our slope intercept equation to solve for b
y = mx + b
3 =
 (6) + b
(6) + b
3 =
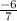 + b Add
+ b Add
 to both sides
to both sides
3 +
 = b
= b
 +
+
 = b
= b
 +
+
 = b
= b
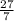 = b
= b
The y-intercept is
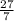 .
.
Now that we have the slope or m (
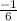 ) and the y-intercept or b (
) and the y-intercept or b (
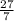 ) we can write the equation
) we can write the equation
y = mx + b
y =
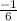 x +
x +
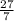
Helping in the name of Jesus.