Question

Determine whether the following equation defines y as a function of x. x² + y² = 7 Does the equation x² + y2 = 7 define y as a function of x? O yes no​

Answer 1

No

Explanation:

No, the equation x² + y² = 7 does not define y as a function of x. This equation represents a circle centered at the origin with a radius of √7. For each value of x, there are two possible values of y (one positive and one negative) that satisfy the equation.

Answer 2

No. The equation x² + y² = 7 does not define y as a function of x.

Explanation:

The equation of a circle is:

`(x - h)^2 + (y - k)^2 = r^2`

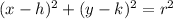
where:

• (x, y) is a point on the circle.
• (h, k) is the center.
• r is the radius.

From observation of the given equation, x² + y² = 7, we can see it represents a circle centered at the origin (0, 0) with a radius of √7.

In a function, for each x-value, there should be a unique y-value.

In the case of a circle, there are two possible y-values for each x-value due to the positive and negative square root.

Therefore, the given equation x² + y² = 7 does not define y as a function of x because it is a circle, and for each x-value there are two possible y-values.