Question

How can the logarithmic expression be rewritten?

Select True or False for each statement.

Answer 1

True

False

True

Explanation:

Use log laws to simplify the left side of each equation.

`\boxed{\begin{minipage}{8cm}\underline{Log laws}\\\\Product law:\quad\:$\log_axy=\log_ax + \log_ay$\\\\Quotient law:\;\;\;$\log_a \left((x)/(y)\right)=\log_ax - \log_ay$\\\\Power law:\quad\;\;\;\:$\log_ax^n=n\log_ax$\\\end{minipage}}`

Given logarithmic statement:

`\log_3v-\log_3w-\log_3x=\log\left((v)/(wx)\right)`

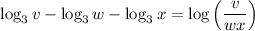
Apply the quotient law for logarithms:

`\begin{aligned}\log_3v-\log_3w-\log_3x&=\log_3\left((v)/(w)\right)-\log_3x\\\\&=\log_3\left(((v)/(w))/(x)\right)\\\\&=\log\left((v)/(wx)\right)\end{aligned}`

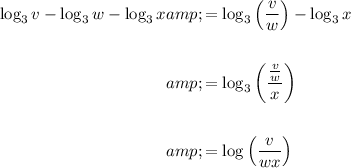
Therefore, the given statement is true.

`\hrulefill`

Given logarithmic statement:

`3\log_4n+\log_4m=\log_4(nm)^3`

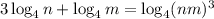
Apply the power law and the product law for logarithms:

`\begin{aligned}3\log_4n+\log_4m&=\log_4n^3+\log_4m\\\\&=\log_4(n^3 \cdot m)\\\\&=\log_4n^3m\end{aligned}`

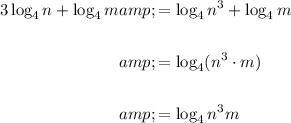
Therefore, the given statement is false.

`\hrulefill`

Given logarithmic statement:

`\log_2\left(\frac{c\sqrt[3]{d}}{e^4}\right)=\log_2c+(1)/(3)\log_2d-4\log_2e`

Apply the quotient law, the product law, and the power law for logarithms:

`\begin{aligned}\log_2\left(\frac{c\sqrt[3]{d}}{e^4}\right)&=\log_2\left(c\sqrt[3]{d}\right) - \log _2\left(e^4\right)\\\\&=\log_2\left(c\right)+\log_2\left(\sqrt[3]{d}\right)-\log _2(e^4)\\\\&=\log_2\left(c\right)+\log_2\left(d^{(1)/(3)}\right)- \log _2(e^4)\\\\&=\log_2c+(1)/(3)\log_2d-4\log_2e\end{aligned}`

Therefore, the given statement is true.