Question

Geometry
Fill in blank and show work

Answer 1

m ∡L =40°

EF = 37.3

Explanation:

Given:

ΔDEF ≅ ΔLMN

We have:

• Respective corresponding side and angle of a congruent triangle are equal or congruent.

For Question:

In ΔDEF and ΔLMN

• DE=LM
• EF=MN
• DF=LN
• m∡D = m ∡L
• m∡E = m ∡M
• m∡F = m ∡N

Let's take DE=LM for side: Note: choose when both sides are known.

DE=LM

• Substitute value

2x+3=53

• subtract both side by 3.

2x+3-3=53-3

2x=50

• Divide both side by 2.

2x/2=50/2

x=25

And let's take m ∡F = m ∡N for angle: Note: choose when both angles are known.

m ∡F = m ∡N

• Substitute value

5y=120°

• Dividing both sides by 5

5y/5=120°/5

y=24

• Since we know value of both x and y.

So,

m ∡L =(x+15)°=(25+15)°=40°

and

EF=1.5y+1.3=1.5*24+1.3=37.3

Answer 2

m∠L = 40°

EF = 37.3

Explanation:

If triangle DEF is congruent to triangle LMN, this means that the two triangles have the exact same shape and size.

Therefore, their corresponding sides and angles are congruent:

`\boxed{\begin{minipage}{2cm}\underline{Sides}\\\\$DE=LM$\\$EF=MN$\\$DF=LN$\\\end{minipage}}`
`\boxed{\begin{minipage}{3cm}\underline{Angles}\\\\$m\angle D = m \angle L$\\$m\angle E= m \angle M$\\$m\angle F = m \angle N$\\\end{minipage}}`

Given that DE = 2x + 3, and LM = 53, then:

`\begin{aligned}DE &=LM\\2x+3&=53\\2x+3-3&=50-3\\2x&=50\\2x / 2&=50/ 2\\x&=25\end{aligned}`

Therefore, the value of x is 25.

Now we have found the value of x, we can substitute it into the expression for angle L to find m∠L:

`\begin{aligned}m \angle L&=(x+15)^(\circ)\\&=(25+15)^(\circ)\\&=40^(\circ)\end{aligned}`

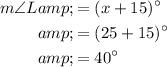
Therefore, m∠L = 40°.

Given that m∠F = 5y° and m∠N = 120°, then:

`\begin{aligned}m \angle F & = m \angle N \\5y^(\circ)&=120^(\circ)\\5y^(\circ) / 5^(\circ)&=120^(\circ) / 5^(\circ)\\y&=24\end{aligned}`

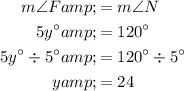
Therefore, the value of y is 24.

Now we have found the value of y, we can substitute it into the expression for side EF:

`\begin{aligned}EF&=1.5y+1.3\\&=1.5(24)+1.3\\&=36+1.3\\&=37.3\end{aligned}`

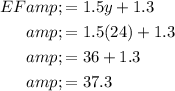
Therefore, EF = 37.3.