Question

!50 POINTS! (3 SIMPLE GEOMETRY QUESTIONS)

QUESTIONS BELOW
|
|
\/

Answer 1

x = 9.7

x = 51.4

x = 4.2

Explanation:

To find the side length labelled "x" in the three given right triangles, we can use trigonometric ratios.

`\boxed{\begin{minipage}{9.4 cm}\underline{Trigonometric ratios} \\\\$\sf \sin(\theta)=(O)/(H)\quad\cos(\theta)=(A)/(H)\quad\tan(\theta)=(O)/(A)$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf O$ is the side opposite the angle. \\\phantom{ww}$\bullet$ $\sf A$ is the side adjacent the angle. \\\phantom{ww}$\bullet$ $\sf H$ is the hypotenuse (the side opposite the right angle). \\\end{minipage}}`

In the first right triangle, angle A = 59°, the side adjacent angle A is b = 5, and the hypotenuse is labelled "x". Therefore, we can use the cosine ratio to find the value of x.

`\cos 59^(\circ)=(5)/(x)`

`x=(5)/(\cos 59^(\circ))`

`x=9.7080201...`

`x=9.7\; \sf (nearest\;tenth)`

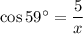
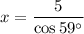
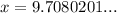
Therefore, the value of x is 9.7, rounded to the nearest tenth.

In the second right triangle, angle A = 79°, the side adjacent angle A is b = 10, and the side opposite angle A is labelled "x". Therefore, we can use the tangent ratio to find the value of x.

`\tan 79^(\circ)=(x)/(10)`

`x=10\tan 79^(\circ)`

`x=51.445540...`

`x=51.4\; \sf (nearest\;tenth)`

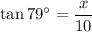
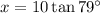
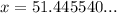
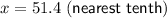
Therefore, the value of x is 51.4, rounded to the nearest tenth.

In the third right triangle, angle A = 72°, the side opposite angle A is b = 13, and the side adjacent angle A is labelled "x". Therefore, we can use the tangent ratio to find the value of x.

`\tan 72^(\circ)=(13)/(x)`

`x=(13)/(\tan 72^(\circ))`

`x=4.223956...`

`x=4.2\; \sf (nearest\;tenth)`

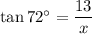
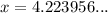
Therefore, the value of x is 4.2, rounded to the nearest tenth.