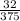Answer:
x =
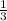 , a₆ =
, a₆ =
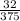
Explanation:
the nth term of a geometric sequence is
 = a₁
= a₁

where a₁ is the first term and r the common ratio
r =
 =
=
 = ... =
= ... =

here a₁ = x + 8 , a₂ = x + 3 and a₃ = x + 1 , then
r =
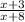 =
=
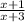 ( cross- multiply )
( cross- multiply )
(x + 3)² = (x + 1)(x + 8) ← expand factors using FOIL
x² + 6x + 9 = x² + 9x + 8 ( subtract x² + 9x from both sides )
- 3x + 9 = 8 ( subtract 9 from both sides )
- 3x = - 1 ( divide both sides by - 3 )
x =
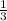
then r =
 =
=
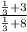 ( multiply numerator/ denominator by 3 to clear the fractions )
( multiply numerator/ denominator by 3 to clear the fractions )
r =
 =
=
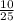 =
=
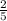
and
a₁ = x + 8 =
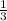 + 8 = 8
+ 8 = 8
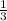 =
=

Then
a₆ =
 ×
×
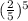 =
=
 ×
×
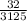 ( cancel 25 and 3125 by 25 )
( cancel 25 and 3125 by 25 )
a₆ =
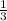 ×
×
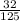 =
=
 =
=