2 Answers

Soham · Answer 1 · 2024-04-08T21:44:19+0000

Answer:

Range of y = 2^x is all positive real numbers.

Range of the function y = 2^{-x} is all positive real numbers excluding zero

Explanation:

Find the range of y = 2^x

Answer:

Since 2^x is an exponential function with a base of 2, the function will always output positive values.

This means that the range of y is all positive real numbers, or y > 0.

In mathematical notation, we can express the range as:

$y \in (0, \infty)$

Therefore, the range of y = 2^x is all positive real numbers .

$\hrulefill$

Find the range of y = 2^(-x)

Answer:

Since 2^{-x} represents the reciprocal of 2^x, the function will output positive values as the exponent becomes more negative.

As x approaches positive infinity
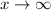$x \to \infty$ , the value of 2^{-x} approaches 0.
As x approaches negative infinity
$x \to -\infty$ , the value of 2^{-x} approaches positive infinity.

Therefore, the range of the function y = 2^{-x} is all positive real numbers greater than zero, but does not include zero itself.

In mathematical notation, we can express the range as:

$y \in (0, \infty)$

Therefore, range of the function y = 2^{-x} is all positive real numbers excluding zero.

Please log in or register to add a comment.