Here we go ~
Formulae to be used here are :
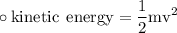
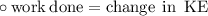
The kinetic energy of cart while moving with velocity 6.0m/s can be calculated as :
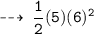
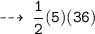
Similarly, kinetic energy at velocity 10.0m/s would be :

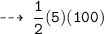
Next up ;
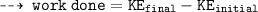
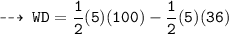
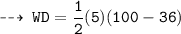
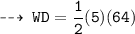
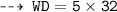
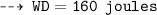
That's our required answer, n matches with choice A.) 160 J