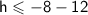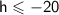Question

What is an inequality for the sum of a number and 12 is at most -8

Answer 1

x ≤ -20

Explanation:

The inequality for the sum of a number and 12 is at most -8 can be written as:

x + 12 ≤ -8

where x is the number we are looking for.

To solve for x, we can subtract 12 from both sides of the inequality:

x ≤ -20

Therefore, the inequality for the sum of a number and 12 is at most -8 can be written as x ≤ -20.

Answer 2

h + 12 ≤ 8

Explanation:

If a number is at most -8, it means it can't be greater than 8, but it can be less than or equal to -8. The symbol for this is ≤.

Next, I'll let h be the number.

Then, the sum of h and 12 is: h + 12

The right side is -8.

We put them together by the ≤ sign.

Therefore, the inequality is:

h + 12 ≤ -8

To solve for h, subtract 12 on each side:

`\sf{h\leqslant-8-12}`

`\sf{h\leqslant-20}`