Question

A savings account was opened 11 years ago with a deposit of $4,570.65. The account has an interest rate of 3.9% compounded monthly. How much interest has the account earned?

$160.08
$181.48
$2,443.71
$7,014.36

Answer 1

C) $2,443.71

Explanation:

To calculate the amount of interest earned on the savings account, use the compound interest formula.

`\boxed{\begin{minipage}{8.5 cm}\underline{Compound Interest Formula}\\\\$ I=P\left(1+(r)/(n)\right)^(nt)-P$\\\\where:\\\\ \phantom{ww}$\bullet$ $I =$ interest accrued.\\ \phantom{ww}$\bullet$ $P =$ principal amount. \\ \phantom{ww}$\bullet$ $r =$ interest rate (in decimal form). \\ \phantom{ww}$\bullet$ $n =$ number of times interest is applied per year. \\ \phantom{ww}$\bullet$ $t =$ time (in years). \\ \end{minipage}}`

Given values:

• P = $4,570.65
• r = 3.9% = 0.039
• n = 12 (monthly)
• t = 11 years

Substitute the given values into the formula and solve for I:

`I=4570.65\left(1+(0.039)/(12)\right)^(12\cdot 11)-4570.65`

`I=4570.65\left(1+0.00325\right)^(132)-4570.65`

`I=4570.65\left(1.00325\right)^(132)-4570.65`

`I=4570.65\left(1.534653130...\right)-4570.65`

`I=7014.362330...-4570.65`

`I=2443.712330...`

`I=\$2,443.71\[ \sf (nearest\;cent)`

Therefore, the amount of interest the account has earned is $2,443.71, rounded to the nearest cent.

Answer 2

$2,443.71

Explanation:

To calculate the interest earned, we can use the formula for compound interest:

`\rm\implies A = P(1 + (r)/(n))^((nt))`

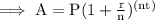
where:

• A = the final amount (including interest)
• P = the principal amount (initial deposit)
• r = the annual interest rate (as a decimal)
• n = the number of times that interest is compounded per year
• t = the number of years

Given:

• P = $4,570.65
• r = 3.9% = 0.039 (as a decimal)
• n = 12 (compounded monthly)
• t = 11 years

Substitute the given values into the above formula:

`\begin{aligned}\rm\implies A& =\rm 4570.65(1 + (0.039)/(12))^((12 \cdot 11))\\& \approx \rm{\$9,014.36}\end{aligned}`

To find the interest earned, we subtract the initial deposit from the final amount:

`\begin{aligned}\rm\implies Interest& =\rm A - P\\& \approx \$9,014.36 - \$4,570.65\\& \approx \boxed{\rm{\$2,443.71}}\end{aligned}`

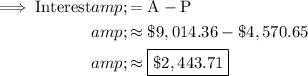
`\therefore` The account has earned $2,443.71 in interest.