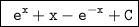Question

∫
`\frac{ {e}^(2x) + {e}^(x) + 1 }{ {e}^(x) } \: dx`
Please help!! ​

Answer 1

(look at the picture)

Answer 2

`\boxed{\tt \:\:e^x + x - e^(-x) + C}`

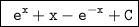
Explanation:

Evaluate the integral step by step:

`\begin{aligned}\tt \int (e^(2x)+e^x+1)/(e^x) dx = \int \left((e^(2x))/(e^x) + (e^x)/(e^x) + (1)/(e^x)\right) dx \\\tt = \int (e^x + 1 + e^(-x)) dx.\end{aligned}`

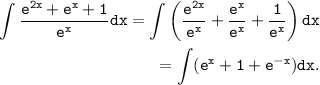
Now, we can integrate each term separately:

1. Integrating
`\tt e^x`:

`\tt \int e^x \:dx = e^x + C_1,`

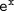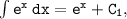
where
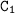`\tt C_1`is the constant of integration.

2. Integrating 1.

`\tt \int 1\ dx = x + C_2,`

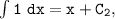
where
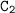`\tt C_2` is another constant of integration.

3. Integrating
`\tt e^(-x).`

`\tt \int e^(-x) \: dx = -e^(-x) + C_3,`

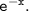
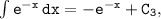
where
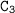`\tt C_3` is a third constant of integration.

Putting it all together, we have:

`\tt \int (e^(2x)+e^x+1)/(e^x) dx = \int (e^x + 1 + e^(-x)) dx \\\tt = \int e^x dx + \int 1 dx + \int e^(-x) dx \\ \tt =(e^x + C_1) + (x + C_2) + (-e^(-x) + C_3) \\\tt = e^x + x - e^(-x) + C`

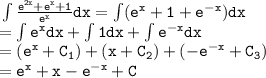
where
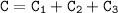`\tt C = C_1 + C_2 + C_3` is the constant of integration.

Therefore, the final solution to the integral
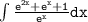`\tt \int (e^(2x)+e^x+1)/(e^x) dx` is
`\boxed{\tt \:\:e^x + x - e^(-x) + C}`