Answer:
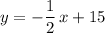 .
.
Explanation:
All non-horizontal line in the cartesian plane intersects the
 -axis at a unique point. The
-axis at a unique point. The
 -coordinate of that point is the
-coordinate of that point is the
 -intercept of this line.
-intercept of this line.
The
 -intercept of the line in this question is
-intercept of the line in this question is
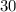 . Thus, the
. Thus, the
 -coordinate of the intersection of this line and the
-coordinate of the intersection of this line and the
 -axis would be
-axis would be
 .
.
Like all other points on the
 -axis, the
-axis, the
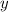 -coordinate of that intersection would be
-coordinate of that intersection would be
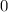 . Therefore, the coordinates of that intersection would be
. Therefore, the coordinates of that intersection would be
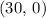 .
.
Similarly, the
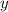 -intercept of a non-vertical line is the
-intercept of a non-vertical line is the
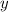 -coordinate of the point where that line intersects the
-coordinate of the point where that line intersects the
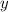 -axis.
-axis.
The slope-intercept form of a line is in the form
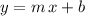 , where
, where
 is the slope of the line and
is the slope of the line and
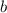 is the
is the
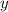 -intercept of this line. Both
-intercept of this line. Both
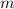 and
and
 are constants.
are constants.
It is given that the
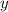 -intercept of the line in this question is
-intercept of the line in this question is
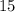 . Therefore,
. Therefore,
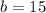 . The slope-intercept equation of this line would be
. The slope-intercept equation of this line would be
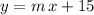 for some slope
for some slope
 to be found.
to be found.
All points
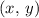 on this line should satisfy the equation
on this line should satisfy the equation
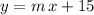 of this line. The
of this line. The
 -intercept of this line,
-intercept of this line,
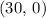 , is a point on this line. Thus, the equation
, is a point on this line. Thus, the equation
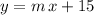 should hold for
should hold for
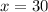 and
and
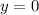 . Substitute these two values into the equation and solve for the slope
. Substitute these two values into the equation and solve for the slope
 :
:
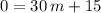 .
.
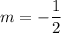 .
.
Therefore, the slope-intercept equation of this line would be:
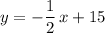 .
.