Question

An electron is near a proton exhibiting a non-uniform electric field. The electron moves to a distance of 2. 5 nm from the proton. What is the electrical potential energy of the electron in this point charge? (-9. 21 x 10-20 J)

(have answer, need work)

Answer 1

Approximately
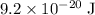`9.2 * 10^(-20)\; {\rm J}` assuming that both particles behave like point charges.

Step-by-step explanation:

In a system consisting of two point charges
`q_(1)` and
`q_(2)` at a distance of
`r` apart from each other, the electrical potential energy of the system would be:

`\displaystyle (k\, q_(1)\, q_(2))/(r)`,

Where
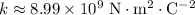`k \approx 8.99* 10^(9)\; {\rm N\cdot m^(2) \cdot C^(-2)}` is the Coulomb Constant.

The electric charge on each proton is equal to the elementary charge: approximately
`1.602 * 10^(-19)\; {\rm C}`. Electric charge on each electron has the same magnitude but the opposite sign: approximately
`(-1.602) * 10^(-19)\; {\rm C}`

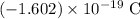
Therefore, in this question, the two charges in the system are:

• 
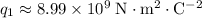  `q_(1) \approx 8.99 * 10^(9)\; {\rm N\cdot m^(2) \cdot C^(-2)}` for the proton, and
• 
  `q_(2) \approx (-8.99) * 10^(9)\; {\rm N\cdot m^(2) \cdot C^(-2)}`.

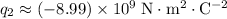Apply unit conversion and ensure that the distance between the two particles is in the standard unit of meters:

`\begin{aligned} r &= 2.5\; {\rm nm} * \frac{1\; {\rm m}}{10^(9)\; {\rm nm}} = 2.5 * 10^(-9)\; {\rm m} \end{aligned}`.

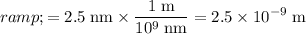Substitute these values into the equation for the electric potential:

`\begin{aligned} & (k\, q_(1)\, q_(2))/(r) \\ \approx \; & ((1.602 * 10^(-19))\, (8.99 * 10^(9))\, (-8.99 * 10^(9)))/((2.5 * 10^(-9)))\; {\rm J} \\ \approx\; & (-9.2) * 10^(-20)\; {\rm J}\end{aligned}`.

In other words, the electric potential of this system would be approximately
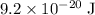`9.2 * 10^(-20)\; {\rm J}`.