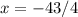Question

Consider the system y=x+11x+3y=1

.

What is the x-coordinate of the solution?

To find out, substitute x + 11 for y in the second equation. Then solve for x. Enter your answers in the boxes.

HELP

Answer 1

Answer: The solution to the equation is
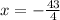`\(x = -(43)/(4)\)`, or -10.75 when expressed as a decimal.

Explanation:

1. Substitute \(y\) in the second equation: The problem asks us to substitute
`\(x + 11\) for \(y\)` in the second equation. This gives us:

`\(x + 11 = 1 - 3y\)`

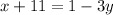
2. Substitute
`\(y\)` with
`\(x + 11\)`: We know that
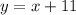`\(y = x + 11\)`, so we substitute
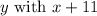`\(y\) with \(x + 11\)` in the equation. This gives us:

`\(x + 11 = 1 - 3(x + 11)\)`

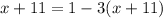
3. Distribute the -3: Next, we distribute the -3 to both
`\(x\)` and 11 inside the parentheses:

`\(x + 11 = 1 - 3x - 33\)`

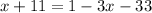
4. Combine like terms: We then combine like terms on the right side of the equation:

`\(x + 11 = -3x - 32\)`

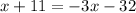
5. Move the x terms to one side: To isolate
`\(x\)`, we move all
`\(x\)` terms to one side of the equation and the constant terms to the other side:

`\(x + 3x = -32 - 11\)`

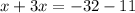
6. Combine like terms again: This gives us:

`\(4x = -43\)`

7. Solve for
`\(x\)`: Finally, we divide both sides by 4 to solve for
`\(x\)`:

`\(x = -43/4\)`