Final Answer:
(a) The net force exerted by the electric field on the dipole is
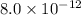 N, directed from the positive to the negative charge.
N, directed from the positive to the negative charge.
(b) The electric dipole moment has a magnitude of
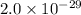 C·m, directed from the negative to the positive charge.
C·m, directed from the negative to the positive charge.
(c) The torque exerted on the dipole is
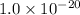 N·m, directed perpendicular to both the electric field and the dipole moment.
N·m, directed perpendicular to both the electric field and the dipole moment.
Explaination:
In the given scenario, an electric dipole is placed in a uniform electric field with a magnitude of
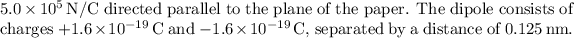
(a) The net force exerted on the dipole is determined by the electric field strength and the separation of charges. The formula
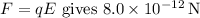 , with the direction from the positive to the negative charge.
, with the direction from the positive to the negative charge.
(b) The electric dipole moment
 is calculated using the formula \
is calculated using the formula \
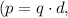 resulting in
resulting in
 directed from the negative to the positive charge.
directed from the negative to the positive charge.
(c)
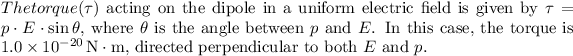
(d) The potential energy
 of the system is given by
of the system is given by
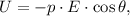 where
where
 is the angle between
is the angle between
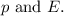 In the given position, the potential energy is not provided, so it cannot be determined without additional information.
In the given position, the potential energy is not provided, so it cannot be determined without additional information.